Котангенс острого угла (ctg): определение, формула, таблица, график, свойства

Понятие угла: радиан, градус

Давай посмотрим на рисунке. Вектор «повернулся» относительно точки на некую величину.

Так вот мерой этого поворота относительно начального положения и будет выступать угол .

Что же ещё необходимо знать о понятии угла?

Ну, конечно же, единицы измерения угла!

Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.

Углом в (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную части окружности.

Таким образом, вся окружность состоит из «кусочков» круговых дуг, или угол, описываемый окружностью, равен .

То есть на рисунке выше изображён угол , равный , то есть этот угол опирается на круговую дугу размером длины окружности.

Углом в радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.

Ну что, разобрался?

Если нет, то давай разбираться по рисунку.

Итак, на рисунке изображён угол , равный радиану, то есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина равна длине или радиус равен длине дуги ).

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A(1, ) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно. 

Для наглядности приведем иллюстрацию.

                                     

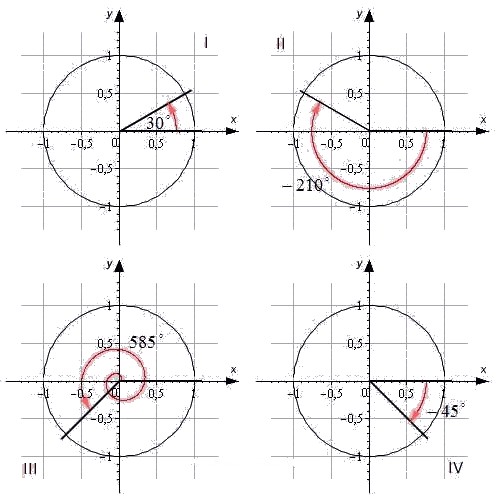
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° —  это угол четвертой четверти.

При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

                                  

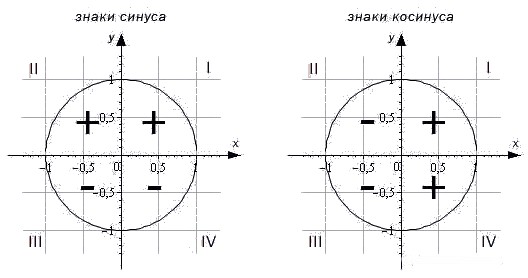
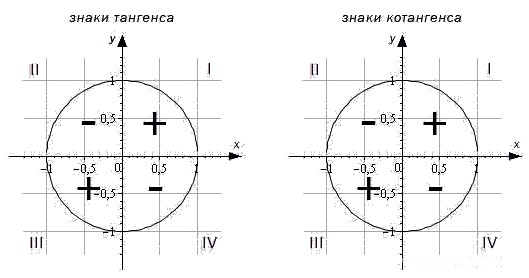
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям. 

                                 

Важно помнить!

1. Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
2. Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
3. Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
4. Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
 

Тождество записывается в следующем виде:
tg α * ctg α = 1.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

1. По определению:
   tg α = y/x
   ctg α = x/y
2. Отсюда следует, что tg α * ctg α = y/x * x/y = 1
3. Преобразовываем выражение, подставляем  и ,
   получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Какие, какие числа?

Взаимно обратные числа — это два числа, произведение которых равно 1.

Применение: тангенс и угол наклона

Пример наклона

Касательная представляет собой важную фигуру для линейных функций : каждая линейная функция

жР.→Р.,Икс↦мИкс+c{\ Displaystyle е \ двоеточие \ mathbb {R} \ to \ mathbb {R}, \; x \ mapsto mx + c}

имеет прямую линию в виде графика . Тангенс (ориентированного) угла между положительным направлением оси x и прямой линией — это наклон прямой линии, т. Е. ЧАС

Неважно, какую из двух полуосей вы выберете в качестве ответной ноги.
α{\ displaystyle \ alpha} м{\ displaystyle m}мзнак равнозагарα{\ Displaystyle м = \ загар \, \ альфа}

Под также понимается тангенс угла уклона. Пример на рисунке справа показывает уклон 10%, соответствующий углу наклона около 5,7 ° с тангенсом 0,1.

Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица.

• ;
• ;
•   ;
• ;
• ;

Название функции	Формула функции	График функции	Название графика	Комментарий
Линейная, прямая пропорциональность	y = kx		Прямая	Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
Линейная, прямая пропорциональность со сдвигом	y = kx + b		Прямая	Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1.
Квадратичная функция	y = x2		Парабола	Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат.
Квадратичная функция	y = ax2 + bx + c		Парабола	Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа
Степенная функция	y = x3		Кубическая парабола	Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Степенная — корень квадратный	y = x1/2		График функцииy = √x	Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Степенная — обратная пропорциональность	y = k/x		Гипербола	Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1.
Показательная функция	y = ex		Экспонента	Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590…
Показательная функция	y = ax		График показательной функции а>1	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1).
Показательная функция	y = ax		График показательной функции 0<a<1	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1).
Логарифмическая функция	y = ln(x)		График логарифмической функции — натуральный логарифм	График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой.
Логарифмическая функция	y = logax		График логарифмической функции — логарифм по основанию а>1	Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1).
Логарифмическая функция	y = logax		График логарифмической функции 0<a<1	Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1).
Синус	y = sinx		Синусоида	Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Косинус	y = cosx		Косинусоида	Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Тангенс	y = tgx		Тангенсоида	Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Котангенс	y = сtgx		Котангенсоида	Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».

Вычисление котангенса числа или любого угла

\(ctg\: t=\)\(\frac{cos\:⁡t}{sin\:⁡t}\)

Пример. Вычислите \(ctg\: \frac{5π}{6}\).Решение: Найдем сначала \(\frac{5π}{6}\) на круге. Затем найдем \(cos\:⁡\frac{5π}{6}\) и \(sin\:\frac{5π}{6}\), а потом поделим одно на другое.

\(ctg\:\frac{5π}{6}=\)\(\frac{cos⁡\:\frac{5π}{6}}{sin⁡\:\frac{5π}{6}}\)\(=-\frac{\sqrt{3}}{2}:\frac{1}{2}=-\frac{\sqrt{3}}{2} \cdot \frac{2}{1}=-\sqrt{3}\)

Ответ: \(-\sqrt{3}\).

Пример. Вычислите \(ctg\:\frac{π}{2}\).

Решение: Чтобы найти котангенс пи на \(2\) нужно найти сначала косинус и синус \(\frac{π}{2}\). И то, и другое найдем с помощью тригонометрического круга:

Точка \(\frac{π}{2}\) на числовой окружности совпадает с \(1\) на оси синусов, значит \(sin\:\frac{π}{2}=1\). Если из точки \(\frac{π}{2}\) на числовой окружности провести перпендикуляр к оси косинусов, то мы попадем в точку \(0\), значит \(cos\:⁡\frac{π}{2}=0\). Получается: \(ctg\:\frac{π}{2}=\)\(\frac{cos\:⁡\frac{π}{2}}{sin\:⁡\frac{π}{2}}\)\(=\)\(\frac{0}{1}\)\(=0\).

Ответ: \(0\).

Пример. Вычислите \(ctg\:(-765^\circ)\).Решение:   \(ctg\: (-765^\circ)=\)\(\frac{cos\:(-⁡765^\circ)}{sin\:⁡(-765^\circ)}\)
Что бы вычислить синус и косинус \(-765^°\). Отложим \(-765^°\) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на \(720^°\) , а потом еще на \(45^°\).

\(sin⁡(-765^°)=-\frac{\sqrt{2}}{2}\);
\(cos⁡(-765^°)=\frac{\sqrt{2}}{2}\) ;
получается \(ctg(-765^°)= \frac{\sqrt{2}}{2} ∶ -\frac{\sqrt{2}}{2}=-1\).

Ответ: \(-1\).

Пример. Найдите \(ctg\:\frac{π}{3}\).Решение:   \(ctg\: \frac{π}{3}=\)\(\frac{cos\:⁡\frac{π}{3}}{sin\:⁡\frac{π}{3}}\). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
\(sin⁡(\frac{π}{3})=\frac{\sqrt{3}}{2}\);
\(cos⁡(\frac{π}{3})=\frac{1}{2}\) ;
получается \(ctg(\frac{π}{3})=\frac{1}{2} ∶ \frac{\sqrt{3}}{2}= \frac{1}{2} \cdot \frac{2}{\sqrt{3}}=\frac{1}{\sqrt{3}}\).

Ответ: \(\frac{1}{\sqrt{3}}\).

Однако можно определять значение котангенса и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:

Ось котангенсов – это фактически копия оси косинусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси косинусов.

Чтобы определить значение котангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу котангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси котангенсов.
3) Найти координату пересечения этой прямой и оси.

Пример. Вычислите \(ctg\:\frac{π}{4}\).Решение:   
1) Отмечаем \(\frac{π}{4}\) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется \(1\).

Ответ: \(1\).

Пример. Найдите значение \(ctg\: 30°\) и \(ctg\: (-60°)\).Решение:   
Для угла \(30°\) (\(∠COA\)) котангенс будет равен \(\sqrt{3}\) (приблизительно \(1,73\)), потому что именно в таком значении сторона угла, проходящая через начало координат и точку \(A\), пересекает ось котангесов.
\(ctg\;(-60°)=\frac{\sqrt{3}}`3`\) (примерно \(-0,58\)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.

Применение в физике

Тангенс и котангенс могут использоваться для описания зависимости скорости от времени, когда тело отбрасывается вверх, если для сопротивления потоку воздуха предполагается турбулентный поток ( трение Ньютона ). Система координат размещена таким образом, чтобы ось местоположения была направлена ​​вверх. Тогда для скорости применяется дифференциальное уравнение вида с ускорением свободного падения g и константой k > 0.
v˙знак равно-грамм-kv2{\ displaystyle {\ dot {v}} = — g-kv ^ {2}}

v(т)знак равноvграмм⋅детская кроватка⁡(граммkт+c)С участиемcзнак равноарккот⁡(v()vграмм)>{\ displaystyle v (t) = v_ {g} \ cdot \ cot ({\ sqrt {gk}} t + c) \ quad {\ text {with}} \ quad c = \ operatorname {arccot} \ left ({ \ frac {v (0)} {v_ {g}}} \ right)> 0},

где — предельная скорость, которая достигается при сопротивлении воздуха . Из-за близких отношений между котангенсом и тангенсом, указанными выше, эта временная зависимость может быть так же легко выражена с помощью тангенса:
vграммзнак равнограммk{\ displaystyle v_ {g} = {\ sqrt {\ frac {g} {k}}}}

v(т)знак равно-vграмм⋅загар⁡(граммkт-c′)С участиемc′знак равноарктан⁡(v()vграмм)>{\ displaystyle v (t) = — v_ {g} \ cdot \ tan \ left ({\ sqrt {gk}} t-c ‘\ right) \ quad {\ text {with}} \ quad c’ = \ arctan \ left ({\ frac {v (0)} {v_ {g}}} \ right)> 0}.

Это решение применяется до тех пор, пока тело не достигнет наивысшей точки своей орбиты (т.е. когда v = 0, то есть для ), после чего необходимо использовать гиперболический тангенс для описания следующего случая с сопротивлением воздуха .
тзнак равноπ2-cграммkзнак равноc′граммk{\ displaystyle t = {\ frac {\ pi / 2-c} {\ sqrt {gk}}} = {\ frac {c ‘} {\ sqrt {gk}}}}

Тригонометрические формулы сложения углов

cos (α — β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α — β) = sin α · cos β — sin β · cos α 
cos (α + β) = cos α · cos β — sin α · sin β 

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Сложный аргумент

загар⁡(Икс+я⋅у)знак равногрех⁡(2Икс)потому что⁡(2Икс)+шиш⁡(2у)+ягрех⁡(2у)потому что⁡(2Икс)+шиш⁡(2у){\ Displaystyle \ загар (х + \ mathrm {я} \! \ cdot \! y) = {\ frac {\ sin (2x)} {\ cos (2x) + \ cosh (2y)}} + \ mathrm { i} \; {\ frac {\ sinh (2y)} {\ cos (2x) + \ ch (2y)}}}   С участием Икс,у∈Р.{\ displaystyle x, y \ in \ mathbb {R}}

детская кроватка⁡(Икс+я⋅у)знак равно-грех⁡(2Икс)потому что⁡(2Икс)-шиш⁡(2у)+ягрех⁡(2у)потому что⁡(2Икс)-шиш⁡(2у){\ Displaystyle \ кроватка (х + \ mathrm {я} \! \ cdot \! y) = {\ frac {- \ sin (2x)} {\ cos (2x) — \ cosh (2y)}} + \ mathrm {i} \; {\ frac {\ sinh (2y)} {\ cos (2x) — \ ch (2y)}}}   С участием Икс,у∈Р.{\ displaystyle x, y \ in \ mathbb {R}}

Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов

Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов и 90 градусов: , а котангенс нуля градусов не определен, и, а тангенс 90 градусов не определен.

В курсе геометрии из прямоугольных треугольников с углами 30, 60 и 90 градусов, а также 45, 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов:,и.

Занесем указанные значения тригонометрических функций для углов , 30, 45, 60 и 90 градусов (, π/6, π/4, π/3, π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.

Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, 330 и 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.

Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.

Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.

График синуса и косинуса

Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток .

Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).

Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.

Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.

Мы знаем, что

sin 0 = 0

sin π/6 = 1/2

sin π/2 = 1

Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:

С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:

Теперь соединим их плавной кривой:

Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:

Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:

Получили ещё два участка графика, на промежутках и . Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:

В результате мы получили кривую, которую называют синусоидой.

Теперь построим график косинуса. Мы знаем что

cos 0 = 1

cos π/3 = 1/2

cos π/2 = 1

Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:

Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:

Соединяем эти точки плавной линией:

Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:

Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток :

Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.

В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:

sin (x+ 2π) = sinx

cos (x+ 2π) = sinx

В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является , а косинус – . Напомним, что ф-ция f(x) является нечетной, если справедливо условие

f(x) = – f(– x)

Если f(x) – четная ф-ция, то должно выполняться условие:

f(x) = f(– x)

Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:

Поэтому верны формулы:

sin (– α) = – sinα

cos (– α) = cosα

Дифференциальное уравнение

Касательная — это решение уравнения Риккати

ш′знак равно1+ш2{\ Displaystyle ш ‘= 1 + ш ^ {2}}.

Факторинг правой стороны дает

ш′знак равно1+ш2знак равно(ш+я)(ш-я){\ Displaystyle вес ‘= 1 + вес ^ {2} = (вес + \ mathrm {i}) (w- \ mathrm {i})}

с мнимой единицей . Касательный (как комплексная функция) имеют исключительные значения , : Эти значения не принимается , поскольку функции постоянных и решение дифференциального уравнения и существования и теорема единственности исключает , что два различных решения имеют то же значение , в том же месте.
я{\ Displaystyle \ mathrm {я}}я{\ Displaystyle \ mathrm {я}}-я{\ displaystyle — \ mathrm {i}}я{\ Displaystyle \ mathrm {я}}-я{\ displaystyle — \ mathrm {i}}

Свойство периодичности

Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.

Свойство периодичности

При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.

Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса. 

Математически данное свойство записывается так: 

sinα+2π·z=sin αcosα+2π·z=cos αtgα+2π·z=tg αctgα+2π·z=ctg α

Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов. 

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем примеры.

sin13π5=sin3π5+2π=sin3π5

tg(-689°)=tg(31°+360°·(-2))=tg31°tg(-689°)=tg(-329°+360°·(-1))=tg(-329°)

Вывод

При выводе тангенса и котангенса появляются менее распространенные тригонометрические функции секанс и котангенс :

ddИксзагар⁡Иксзнак равно1+загар2⁡Иксзнак равно1потому что2⁡Иксзнак равносек2⁡Икс{\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ tan x = 1 + \ tan ^ {2} x = {\ frac {1} {\ cos ^ {2} x }} = \ сек ^ {2} x}

ddИксдетская кроватка⁡Иксзнак равно-1-детская кроватка2⁡Иксзнак равно-1грех2⁡Иксзнак равно-csc2⁡Икс{\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ cot x = -1- \ cot ^ {2} x = — {\ frac {1} {\ sin ^ {2 } x}} = — \ csc ^ {2} x}

В их производных могут быть выражены с помощью функции полигаммы :
п{\ displaystyle n}

dпdИкспзагар⁡Иксзнак равноψп(12+Иксπ)-(-1)пψп(12-Иксπ)πп+1{\ displaystyle {\ frac {\ mathrm {d} ^ {n}} {\ mathrm {d} x ^ {n}}} \ tan x = {\ frac {\ psi _ {n} ({\ tfrac {1 } {2}} + {\ tfrac {x} {\ pi}}) — (- 1) ^ {n} \, \ psi _ {n} ({\ tfrac {1} {2}} — {\ tfrac {x} {\ pi}})} {\ pi ^ {n + 1}}}}

dпdИкспдетская кроватка⁡Иксзнак равно(-1)пψп(1-Иксπ)-ψп(Иксπ)πп+1{\ displaystyle {\ frac {\ mathrm {d} ^ {n}} {\ mathrm {d} x ^ {n}}} \ cot x = {\ frac {(-1) ^ {n} \, \ psi _ {n} (1 — {\ tfrac {x} {\ pi}}) — \ psi _ {n} ({\ tfrac {x} {\ pi}})} {\ pi ^ {n + 1}} }}