Как найти число зная среднее арифметическое

Расчет среднего значения по условию

Кроме обычного расчета среднего значения, имеется возможность подсчета среднего значения по условию. В этом случае, в расчет будут браться только те числа из выбранного диапазона, которые соответствуют определенному условию. Например, если эти числа больше или меньше конкретно установленного значения.

Для этих целей, используется функция «СРЗНАЧЕСЛИ». Как и функцию «СРЗНАЧ», запустить её можно через Мастер функций, из панели формул, или при помощи ручного ввода в ячейку. После того, как открылось окно аргументов функции, нужно ввести её параметры. В поле «Диапазон» вводим диапазон ячеек, значения которых будут участвовать в определении среднего арифметического числа. Делаем это тем же способом, как и с функцией «СРЗНАЧ».

А вот, в поле «Условие» мы должны указать конкретное значение, числа больше или меньше которого будут участвовать в расчете. Это можно сделать при помощи знаков сравнения. Например, мы взяли выражение «>=15000». То есть, для расчета будут браться только ячейки диапазона, в которых находятся числа большие или равные 15000. При необходимости, вместо конкретного числа, тут можно указать адрес ячейки, в которой расположено соответствующее число.

Поле «Диапазон усреднения» не обязательно для заполнения. Ввод в него данных является обязательным только при использовании ячеек с текстовым содержимым.

Когда все данные введены, жмем на кнопку «OK».

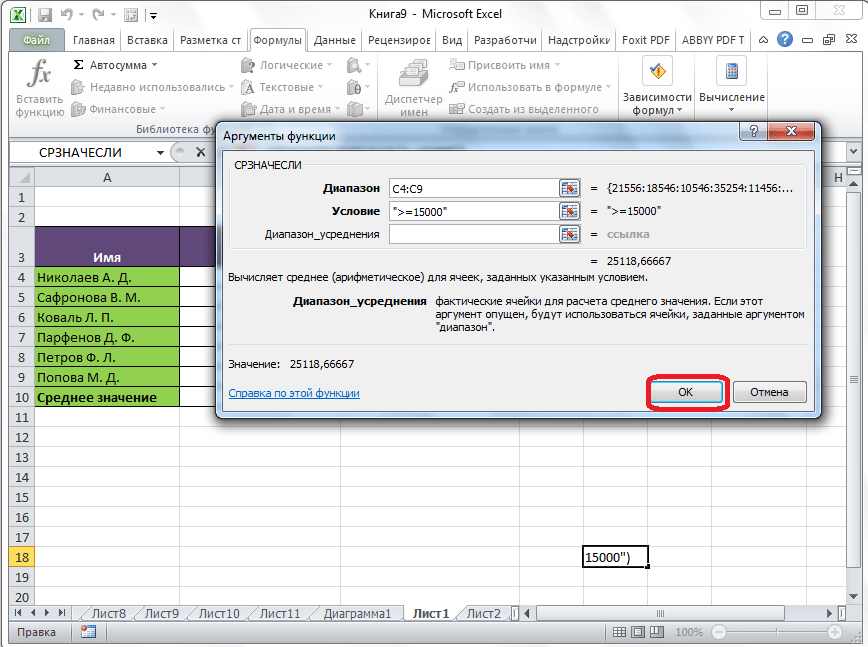
После этого, в предварительно выбранную ячейку выводится результат расчета среднего арифметического числа для выбранного диапазона, за исключением ячеек, данные которых не отвечают условиям.

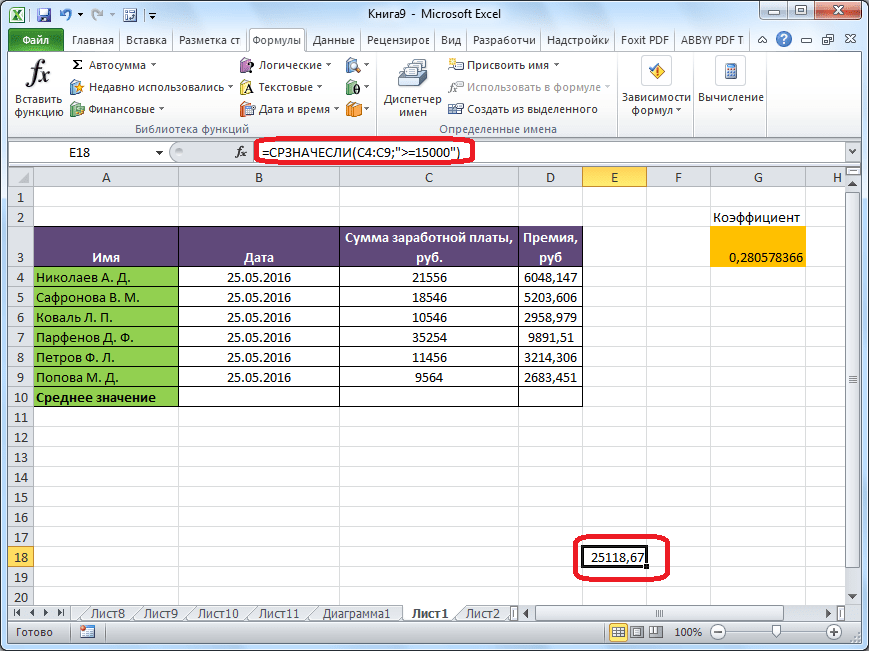
Как видим, в программе Microsoft Excel существует целый ряд инструментов, с помощью которых можно рассчитать среднее значение выбранного ряда чисел. Более того, существует функция, которая автоматически отбирает числа из диапазона, не соответствующие заранее установленному пользователем критерию. Это делает вычисления в приложении Microsoft Excel ещё более удобными для пользователей.

Как считать средние для разнородных данных

В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12

Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.

Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.

Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.

Как найти среднее значение в Excel?

Ситуация такая. Имеется следующая таблица:
В столбиках, закрашенных красным цветом содержатся численные значения оценок по предметам. В столбце «Средний балл» требуется подсчитать их среднее значение.
Проблема вот в чем: всего предметов 60-70 и часть из них на другом листе.
Я смотрела в другом документе уже подсчитано среднее, а в ячейке стоит формула типа
=’имя листа’!|Е12
но это делал какой-то программист, которого уволили.
Подскажите, пожалуйста, кто разбирается в этом.

Гектор

В строке фцнкций вставляешь из предложеннвх функций «СРЗНАЧ» и выбираешь откуда те надо высчитать (B6:N6) для Иванова, к примеру. Про соседние листы точно не знаю, но наверняка это содержится в стандартной виндовской справке

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:

1. Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
2. Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.

Формула

Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:

В данной формуле переменные имеют следующее значение:

А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.

Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.

Расчет среднего арифметического

Введите исходные данные

Введите число

Сохранить исходный ряд данныхупорядочить данные по возрастаниюупорядочить данные по убываниювернуть исходную последовательность

Что-то пошло не так…
Прямое восхождение не может быть больше 24 часов,
минуты и секунды больше 60,
а склонение по абсолютной величине не должно быть больше 90°

OK

Среднее арифметическое, a_ср

Дисперсия, σ2

Среднеквадратическое отклонение, σ

Коэффициент вариации, V

Размах вариации, R

Среднее линейное отклонение, δ

Design by Sergey Ov for abc2home.ru

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднего арифметического в истории браузера

Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднего арифметического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

• Среднее арифметическое — расчет онлайн, определение, формула
• Среднеквадратическое отклонение — расчет онлайн, определение, формула
• Среднее геометрическое — расчет онлайн, определение, формула
• Среднее гармоническое и среднее степенное — расчет онлайн, определения, формулы
• Среднее квадратическое — расчет онлайн, определение, формула

Рассмотрим пару примеров

Расчет средней оценки

Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:

(3 + 3 + 5 + 4) / 4 = 3,75

Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.

Расчет съеденных конфет

Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу

Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных

Способ стандартный

Первостепенно разберем способ, как посчитать среднее арифметическое в Excel, который подразумевает использование стандартного инструмента для этого. Метод является наиболее простым и удобным для использования, однако у него существуют и некоторые недостатки. Но о них позже, а сейчас перейдем к выполнению поставленной задачи.

1. Выделите ячейки столбца или строки, в которых находятся числовые значения для расчета.
2. Перейдите во вкладку «Главная».
3. На панели инструментов в категории «Редактирование» нажмите по кнопке «Автосумма», однако жать необходимо на стрелочку рядом с ней, чтобы появился выпадающий список.
4. В нем вам необходимо кликнуть по пункту «Среднее».

Как только вы это сделаете, в ячейке рядом появится результат расчета среднего арифметического выделенных значений. Его расположение будет зависеть от блока данных, если вы выделили строку, то находиться результат будет справа от выделения, если столбец, снизу.

Но как было сказано ранее, у данного метода есть и недостатки. Так, у вас не получится рассчитать значение из диапазона ячеек, или же ячеек, расположенных в разных местах. Например, если в вашей таблице смежно находятся два столбца с числовыми значениями, то, выделив их и произведя вышеописанные действия, вы получите результат для каждого столбца в отдельности.

Как посчитать среднее значение в Ворде?

Как в Ворде найти среднее значение в одном или нескольких столбцах таблицы?

Понятно, что можно скопировать её в Эксель и посчитать среднее там.

Но можно ли сделать это непосредственно в документе Ворд?

Конечно можно, но пересчитываться автоматически не будет, что может стать источником ошибок.

Сначала надо нарисовать таблицу с числами, щелкнуть мышкой в ячейку где будет записано среднее значение и тогда в верхнем меню появится пункт Макет.

Надо выбрать Макет\Формула

В открывшемся окне выбираем функцию высчитывания среднего значения AVERAGE и ставим аргумент ABOVE (ABOVE — считать ячейки выше той в которой записана формула)

Нажимаем ОК и получаем результат

Если нужно рассчитать среднее по диапазону, то пишем как в Экселе из расчета , что первая строка таблицы имеет номер 1, первый столбец таблицы обозначается A ,например B2:C4.

При изменении данных таблицы придется принудительно обновить поле

Для обновления всех полей в выделенной области надо нажать F9 (например выделить всю таблицу и нажать F9)

Чтобы исключить ошибки, желательно в параметрах Word установить в разделе Экран галочку Обновлять поля перед печатью

Как вычислить среднее арифметическое и среднее геометрическое чисел

Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6?

Решение: (11 + 4 + 3) / 3 = 6

В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три.

Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8.

Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось:

Решение: ∛(4 × 2 × 8) = 4

В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое — ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30.

Если в массиве есть числа в текстовом формате

В случае, если число введено в ячейку с текстовым форматом (см. ячейку А6 ), то это значение воспринимается функцией СРЗНАЧ() как текст и игнорируется. Поэтому, не смотря на то, что в диапазоне A 5: A 15 11 значений, для функции СРЗНАЧ() их всего 10, т.е. n в этом случае =10. Среднее будет равно 20,4 (см. файл примера ).

Функция СРЗНАЧA() ведет себя по другому: числа в текстовом формате интерпретируются ею как 0, впрочем, как и все остальные текстовые значения, включая значение Пустой текст “” . Поэтому, для функции СРЗНАЧА() n =11, а среднее будет равно 18,545454.

Чтобы числа в текстовом формате также учитывались при вычислении среднего, то нужно записать формулу массива =СРЗНАЧ(A5:A15+0) . В этом случае среднее будет равно 18,818181, т.к. n=11, а число в текстовом формате будет интерпретировано как 3.

Примечание : Чтобы перевести числа из текстового формата в числовой см. статью Преобразование ЧИСЕЛ из ТЕКСТового формата в ЧИСЛОвой (Часть 1. Преобразование формулами) .

Примечание : о вычислении средневзвешенного значения см. статью Средневзвешенная цена в MS EXCEL

Подсчет среднего арифметического

Формула для вычислений предельно проста:

P = (a1 + a2 + … an) / n,

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.

Среднее значение по условию

Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().

Найти среднее арифметическое чисел, которые больше или равны 10.

Функция: =СРЗНАЧЕСЛИ(A1:A8;”>=10″)

Результат использования функции СРЗНАЧЕСЛИ по условию “>=10”:

Третий аргумент – «Диапазон усреднения» – опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.

Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку

Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».

Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово “столы”). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.

В результате вычисления функции получаем следующее значение:

Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно

Мода

Допустим, вы планируете вечеринку и нужно назначить день недели для её проведения. Дни недели — такой же числовой ряд, как и любой другой. Это всего лишь числа от 1 до 7. Среднее арифметическое и медиана тут не помогут (Лиза и Паша могут в пятницу, а Коля и Петя — в воскресенье; поэтому назначим субботу). Что делать? Конечно, выбрать тот день недели, который выберет большинство, ну а остальные либо подстроятся, либо не придут — демократия, однако.

Прелести моды: Прекрасно работает для получения представления об общественном мнении; Даёт представление о потребностях большой части людей (там, где среднее арифметическое даёт лишь осечку); Проста для понимания.

Изъяны моды: Для её вычисления требуется больше усилий (нужно собрать мнения и обработать их); Победителю достаётся всё: мода выявляет только одного лидера.

Как считать средние для разнородных данных

В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12

Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.

Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.

Определение среднего значения по условию

Помимо перечисленных выше методов, в Эксель также предусмотрена возможность расчета среднего значения по заданному пользователем условию. Как следует из описания, участвовать в общем подсчете будут только числа (ячейки с числовыми данными), соответствующие какому-то конкретному условию.

Допустим, нам нужно посчитать среднее значение только по положительным числам, т.е. тем, которые больше нуля. В этом случае, нас выручит функция СРЗНАЧЕСЛИ.

1. Встаем в результирующую ячейку и жмем кнопку “Вставить функцию” (fx) слева от строки формул.
2. В Мастере функций выбираем категорию “Статистические”, кликаем по оператору “СРЗНАЧЕСЛИ” и жмем ОК.
3. Откроются аргументы функции, после заполнения которых кликаем OK:
   • в значении аргумента “Диапазон” указываем (вручную или выделив с помощью левой кнопки мыши в самой таблице) требуемую область ячеек;
   • в значении аргумента “Условие”, соответственно, задаем наше условие попадания ячеек из отмеченного диапазона в общий расчет. В нашем случае, это выражение “>0”. Вместо конкретного числа, в случае необходимости, в условии можно указать адрес ячейки, содержащей числовое значение.
   • поле аргумента “Диапазон_усреднения” можно оставить пустим, так как его обязательное заполнение требуется только при работе с текстовыми данными.
4. Среднее значение с учетом заданного нами условия отбора ячеек отобразилось в выдранной ячейке.

Общие сведения

Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:

1. Целые.
2. Дробные.

Первый тип — натуральные числа, они применяются при устном счете предметов.

Дробные бывают также двух типов:

1. Десятичными.
2. Обыкновенными.

Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.

В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.

Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.

Классический подход

Как ни странно, большинство решений в сети выглядит, как последовательный перебор всех групп размером (например 4) и вычисление среднего для каждой:

Безусловно, это решение работает, но оно очень плохое. Здесь происходит огромное количество повторных вычислений и лишних операций. Разберем весь код по порядку и посмотрим, строка за строкой, что происходит «под капотом».

Создание массива в JavaScript, выделяет определенную область памяти для хранения данных. Размер массива не определенный и он наполняется по мере работы цикла, в какой-то момент может наступить заполнение выделенной области памяти и модуль управления памятью будет вынужден выделить новоую, более широкую область, затем осуществить перенос в нее диапазона всех значений памяти из предыдущей области, в разных движках это может работать по разному, но в любом случае необходимо, как минимум, выделение новой области памяти. И вот, как выглядит график замера времени на операцию push, в зависимости от длинны массива.

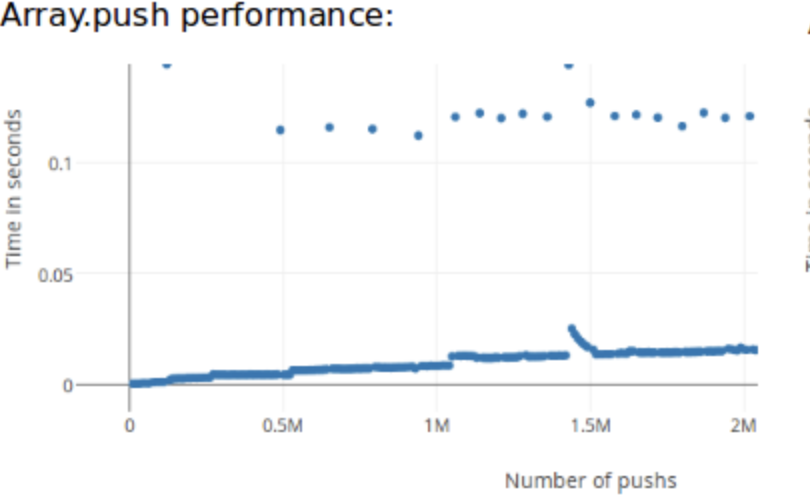
На картинке видны космические, по местным масштабам выбросы. Это происходит по причине тех самых накладных работ в памяти движка на перенос всей области, либо на выделение новой области и связывание со старой.

Из этого можно сделать два вывода:

1. Для работы с большими массивами лучше использовать создание массива через конструктор как: . Это позволит вам задать размер массива и движок выделит столько памяти, сколько нужно.

2. А зачем тут этот массив вообще. (Позже мы к этому вернемся)

Для начала, ремарка про цикл. Я бы не стал так подробно мусолить цикл и перешел бы к следующей части, тк в целом оптимизация цикла не дала бы нужный эффект производительности, но это просто крик души, ода к безграмотности современных разработчиков, щепетильно пишущих бенчмарки налево и направо.Погуглив «Самый быстрый способ итерации в JavaScript» не трудно наткнуться на кучу разных бенчмарков, которые написаны не правильно. Почему не правильно? .

В теории самый самый быстрый способ итерации в JavaScript － , но все тесты в лучшем случае предлагают такой вариант условия остановки: , в котором добавляется дополнительная нагрузка в виде приведения типа числа из в . Даже такой вариант выхода из цикла не совсем правильный: потому, что сравнение с 0 является одной из самых быстрых операций и отличается от сравнения с любыми другими видами чисел.Бытует мнение, что это миф, однако это не так. Доказательство очень простое, взглянем как процессор обрабатывает сравнение с 0 и с 1

Обратите внимание на 5ую строку. Там используется сравнение

Которое вежливо отмечено вторым в порядке быстродействия самими разработчиками v8.

Выводы:

1. Сравнение с нулем или нет — разница есть!

2. Не верьте бенчмаркам, если они написаны не правильно

3. Все эти вычисления можно сделать без цикла, об этом позже.

Теперь очередь этой строки. Оператор создает новый массив, для которого выделяется память, заполняет его данными из предыдущего массива (иммутабильно) и присваивается в переменную chunk. Это с ума сойти сколько операций на пустом месте. И тут все можно описать столь же подробно, но я не стану, потому что больше нет сил разбираться в рубрике «По колено в коде» (Олды тут?). Выше, я все обещал позже рассказать о том, как сделать эти вычисления эффективнее. Приступим!

Средневзвешенное значение — что это и как его вычислить?

В процессе изучения математики школьники знакомятся с понятием среднего арифметического. В дальнейшем в статистике и некоторых других науках студенты сталкиваются и с вычислением других средних значений. Какими они могут быть и чем отличаются друг от друга?

Средние величины: смысл и различия

Не всегда точные показатели дают понимание ситуации. Для того чтобы оценить ту или иную обстановку, нужно подчас анализировать огромное количество цифр. И тогда на помощь приходят средние значения. Именно они позволяют оценить ситуацию в общем и целом.

Часто в рамках школьного курса изучают и среднее геометрическое. Расчет данного значения базируется на извлечении корня n-ной степени из произведения n-членов. Если брать те же числа: 27, 22, 34 и 37, то результат вычислений будет равен 29,4.

Среднее гармоническое в общеобразовательной школе обычно не является предметом изучения. Тем не менее оно используется довольно часто. Эта величина обратна среднему арифметическому и рассчитывается как частное от n — количества значений и суммы 1/a₁+1/a₂+…+1/a_n. Если снова брать тот же ряд чисел для расчета, то гармоническое составит 29,6.

Средневзвешенное значение: особенности

Однако все вышеперечисленные величины могут быть использованы не везде. Например, в статистике при расчете некоторых средних значений важную роль имеет «вес» каждого числа, используемого в вычислениях. Результаты являются более показательными и корректными, поскольку учитывают больше информации. Эта группа величин носит общее название «средневзвешенное значение». Их в школе не проходят, поэтому на них стоит остановиться поподробнее.

Прежде всего, стоит рассказать, что подразумевается под «весом» того или иного значения. Проще всего объяснить это на конкретном примере. Два раза в день в больнице происходит замер температуры тела у каждого пациента. Из 100 больных в разных отделениях госпиталя у 44 будет нормальная температура — 36,6 градусов. У еще 30 будет повышенное значение — 37,2, у 14 — 38, у 7 — 38,5, у 3 — 39, и у двух оставшихся — 40. И если брать среднее арифметическое, то эта величина в общем по больнице будет составлять больше 38 градусов! А ведь почти у половины пациентов совершенно нормальная температура. И здесь корректнее будет использовать средневзвешенное значение, а «весом» каждой величины будет количество людей. В этом случае результатом расчета будет 37,25 градусов. Разница очевидна.

В случае средневзвешенных расчетов за «вес» может быть принято количество отгрузок, число работающих в тот или иной день людей, в общем, все что угодно, что может быть измерено и повлиять на конечный результат.

Разновидности

Средневзвешенное значение соотносится со средним арифметическим, рассмотренным в начале статьи. Однако первая величина, как уже было сказано, учитывает также вес каждого числа, использованного в расчетах. Помимо этого существуют также средневзвешенное геометрическое и гармоническое значения.

Имеется еще одна интересная разновидность, используемая в рядах чисел. Речь идет о взвешенном скользящем среднем значении. Именно на его основе рассчитываются тренды. Помимо самих значений и их веса там также используется периодичность. И при вычислении среднего значения в какой-то момент времени также учитываются величины за предыдущие временные отрезки.

Расчет всех этих значений не так уж и сложен, однако на практике обычно используется только обычное средневзвешенное значение.

Способы расчета

В век повальной компьютеризации нет необходимости вычислять средневзвешенное значение вручную. Однако нелишним будет знать формулу расчета, чтобы можно было проверить и при необходимости откорректировать полученные результаты.

Проще всего будет рассмотреть вычисление на конкретном примере.

Заработная плата (тыс. руб.)	Число рабочих (чел.)
32	20
33	35
34	14
40	6

Необходимо узнать, какая же средняя оплата труда на этом предприятии с учетом количества рабочих, получающих тот или иной заработок.

Итак, расчет средневзвешенного значения производится с помощью такой формулы:

x = (a₁*w₁+a₂*w₂+…+a_n*w_n)/(w₁+w₂+…+w_n)

Для примера же вычисление будет таким:

x = (32*20+33*35+34*14+40*6)/(20+35+14+6) = (640+1155+476+240)/75 = 33,48

Очевидно, что нет особых сложностей с тем, чтобы вручную рассчитать средневзвешенное значение. Формула же для вычисления этой величины в одном из самых популярных приложений с формулами — Excel — выглядит как функция СУММПРОИЗВ (ряд чисел; ряд весов)/СУММ (ряд весов).

fb.ru

В чём фокус?

Среднее гармоническое действительно не самая очевидная вещь. Дело в том, что если бы у вас было две разных установки, одна из которых работает со скоростью 10 деталей/час, а другая — 20 деталей/час, конечно, их средняя производительность составляла бы 15 деталей/час. В этом случае вы имеете полное право просто сложить их производительность и вычислить среднее арифметическое, ведь установки работают независимо друг от друга.

Если не верите в среднее гармоническое, можно устроить себе обратную проверку. Мы утверждаем, что наша универсальная установка по заготовке и полировке деталей справляется с 7,14 деталями в час. Проверим: мы знаем, что за час машина либо обрабатывает 25 деталей, либо полирует 10. Получаем:

Подготовка: 7,14/25 = 0,29 часов Полировка: 7,14/10 = 0,71 часов

Да-да, 0,29 + 0,71 = 1, цифры работают: для полного цикла изготовления 7,14 деталей действительно требуется один час.

Средняя арифметическая взвешенная

Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч. 

Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:

Теперь преобразуем формулу до удобного вида.

Подставим значения.

Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.

Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.

где x – анализируемый показатель; f – вес.

Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую. 

Пример решения

Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.

Решение выполняется по следующему алгоритму:

1. Записать величины: 3 2/3, 4 5/7 и 6 3/8.
2. Количество: 3.
3. Конвертировать их в неправильные дроби: 11/3, 33/7 и 51/8.
4. Привести к единому знаменателю: (11*56)/168=616, 33*24/168=792 и 51*21/168=1071/168.
5. Вычислить сумму: 2479/168.
6. Определить среднее арифметическое: (2479/168):3=(2479/168)*1/3=2479/504.
7. Преобразовать в смешанное дробное выражение: 2479/504=4 463/504.
8. Значение искомой величины равно 4 463/504.

При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.

Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.

Найти среднее значение в excel формула

Excel предсталяет собой табличный процессор. Его можно использовать для создания разнообразных отчетов. В данной программе очень удобно производить разные вычисления. Многие не используют и половину возможностей Excel.

Найти средние значение чисел может понадобиться в школе, а также во время работы. Классическим способ определения среднего арифметического без использования программ заключается в складывании всех чисел, а затем полученную сумму нужно разделить на количество слагаемых. Если числа достаточно крупные или для отчетности необходимо выполнить операцию много раз, вычисления могут занять много времени. Это нерациональная трата сил и времени, намного лучше воспользоваться возможностями Excel.

Подсчёт среднего арифметического пары

Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:

1. Первоначально требуется провести операцию сложения выбранных чисел. Это часто можно сделать, как говорится, вручную, не используя электронную технику.
2. После того как сложение произведено и получен его результат необходимо произвести деление. Данная операция подразумевает разделение суммы двух сложенных чисел на два – количество сложенных чисел. Именно такое действие и позволит получить требуемую величину.

Формула

Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:

(А+В)/2

В этой формуле применяется следующее обозначение:

А и В – это заранее выбранные числа, для которых необходимо находить значение.