Как сделать знак умножить

Умножение дробей

Умножьте вершины, умножьте основания.

https://youtube.com/watch?v=_7iIvH0GCdU

Есть 3 простых шага для умножения дробей

1. Умножьте верхние числа (числители ).

2. Умножьте нижние числа (знаменатели ).

3. При необходимости упростите дробь.

Пример:

1 2 × 2 5

Шаг 1 .Умножьте верхние числа:

1 2 × 2 5 знак равно 1 × 2 знак равно 2

Шаг 2 . Умножаем нижние числа:

1 2 × 2 5 знак равно 1 × 2 2 × 5 знак равно 2 10

Шаг 3 .Упростим дробь:

2 10 знак равно 1 5

Другой пример:

1 3 × 9 16

Шаг 1 .Умножьте верхние числа:

1 3 × 9 16 знак равно 1 × 9 знак равно 9

Шаг 2 . Умножаем нижние числа:

1 3 × 9 16 знак равно 1 × 9 3 × 16 знак равно 9 48

Шаг 3 .Упростим дробь:

9 48 знак равно 3 16

(На этот раз мы упростили, разделив верхнюю и нижнюю части на 3)

Рифма

♫ «Умножение дробей: нет большой проблемы, Верхнее умножение сверху на нижнее умножение на низ. « И не забудьте упростить, Прежде, чем пришло время прощаться »♫

Дроби и целые числа

А как насчет умножения целых чисел на дроби и ?

Превратите целое число в дробь, поставив его над единицей.

Затем продолжайте как раньше.

Пример:

2 3 × 5

Превратите 5 в 5 1 :

2 3 × 5 1

А теперь как обычно.

Умножение вершин и оснований:

2 3 × 5 1 знак равно 2 × 5 3 × 1 знак равно 10 3

Дробь уже настолько проста, насколько это возможно.

Ответ = 10 3

Или вы можете просто представить себе целое число как «верхнее» число:

Пример:

3 × 2 9

Умножение вершин и оснований:

3 × 2 9 знак равно 3 × 2 9 знак равно 6 9

6 9 знак равно 2 3

Вы также можете прочитать, как умножить смешанные дроби

Изменение произведения чисел при изменении его сомножителей

Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких сомножителей, нужно вспомнить, что действие умножения – это частный случай действия сложения, а также переместительный и сочетательный законы сложения.

Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.

Рассмотрим пример 18 ∙2. Увеличив второй сомножитель, к примеру, в 3 раза, мы получим другое выражение: 18 ∙6.

Действительно:

18 ∙2 =3618 ∙6 =108.

Если мы увеличим 36 в 3 раза, то мы получим как раз 108.

По-другому и быть не может, и вот почему.

Первое произведение представляет собой сумму двух слагаемых:

18+18.

Второе произведение – это сумма шести таких же слагаемых:

18+18+18+18+18+18.

Если мы, воспользовавшись сочетательным законом умножения, сгруппируем эти слагаемые по 2, то получим следующее:

(18+18)+(18+18)+(18+18).

Как видите, у нас получилось 3 одинаковых слагаемых, каждый из которых равен первому произведению. А это значит, что полученное произведение состоит из трех, которые были даны изначально, то есть, в 3 раза больше начального. Что и требовалось доказать.

Для второго сомножителя справедливость этого свойства доказывается на основе переместительного закона умножения.

Если уменьшить один из сомножителей в несколько раз, произведение также уменьшится в это же число раз.

Если увеличить один из сомножителей в несколько раз, а второй в это же число раз уменьшить, то произведение при этом не поменяется.

Действительно, при увеличении одного из сомножителей , а при уменьшении другого сомножителя . Поэтому, если увеличить одно и одновременно уменьшить другое число, то эти изменения компенсируют друг друга, и произведение :

32 ∙8 =256,

Увеличим первый сомножитель в 4 раза, а второй во столько же раз уменьшим:

128 ∙2 =256.

Теперь уменьшим первый сомножитель произведения 32 ∙8 в 4 раза, а второй уменьшим в это же число раз:

8 ∙32 =256.

Правило умножения чисел с разными знаками

Определение 1

Для того, чтобы произвести действие умножения чисел с разными знаками, необходимо перемножить модули заданных чисел и полученному результату присвоить знак минус.

Запишем указанное правило в виде равенства. Пусть заданы любое действительное положительное число a и любое действительное отрицательное число –b. Тогда правило умножения будет выглядеть следующим образом: a·(-b) =-(|a|·|b|). Если задано отрицательное число –aи положительное число b, справедливо будет равенство(-a)·b=-(|a|·|b|).

Правило перемножения чисел с различными знаками в полной мере соответствует свойствам действий с действительными числами. Опираясь на них, возможно продемонстрировать, что для любых действительных положительных чисел a и b будет справедливой следующая цепочка равенств: a·(-b) +a·b=a·((-b)+ b)=a·=. Эта цепочка является доказательством того, что a·(- b)иa·b — противоположные числа, а значит a·(- b)=-(a·b). Из последнего равенства и следует справедливость указанного выше правила.

Отметим, что рассматриваемое правило перемножения чисел с различными знаками распространяется не только на действительные числа, но и рациональные и целые. Такой вывод можно сделать, опираясь на то, что действия с рациональными и целыми числами имеют те же свойства, что мы использовали при доказательстве правила.

По сути, умножение чисел с различными знаками по правилу, указанному выше, приводит к перемножению положительных чисел.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:

Два главных определения:

Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.

Запоминаем!

Положительные числа — это те, что больше нуля, а отрицательные — меньшие.

Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:

Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения От перестановки множителей местами произведение не меняется. a * b = b * a Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением. a * b * c = (a * b) * c = a * (b * c)

Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор. 

История

Самый старый из используемых символов умножения — косой крестик (×). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» (1631, Лондон). До него использовали чаще всего букву M, предложенную в 1545 году Михаэлем Штифелем и поддержанную Симоном Стевином. Позднее предлагались и другие обозначения:

• латинское слово in (Франсуа Виет);
• символ прямоугольника в начале произведения и запятую в конце (Эригон, 1634);
• звёздочку (Иоганн Ран, она появилась в его книге «Teutsche Algebra», 1659);
• букву x (в одном из трудов Валлиса,1655); возможно, это типографская ошибка, так как на одной странице у Валлиса встречаются и буква x, и косой крестик.

Готфрид Лейбниц, поэкспериментировав с несколькими разными символами, в конце концов решил заменить крестик на точку (1698 год), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и Томаса Хэрриота. Многие математики, начиная с Диофанта, вместо знака умножения просто записывали операнды подряд.

Первое правило раскрытия скобок

Рассмотрим выражение:

8 + (−9 + 3)

Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак. Формула раскрытия скобок (a − b) = a — b

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

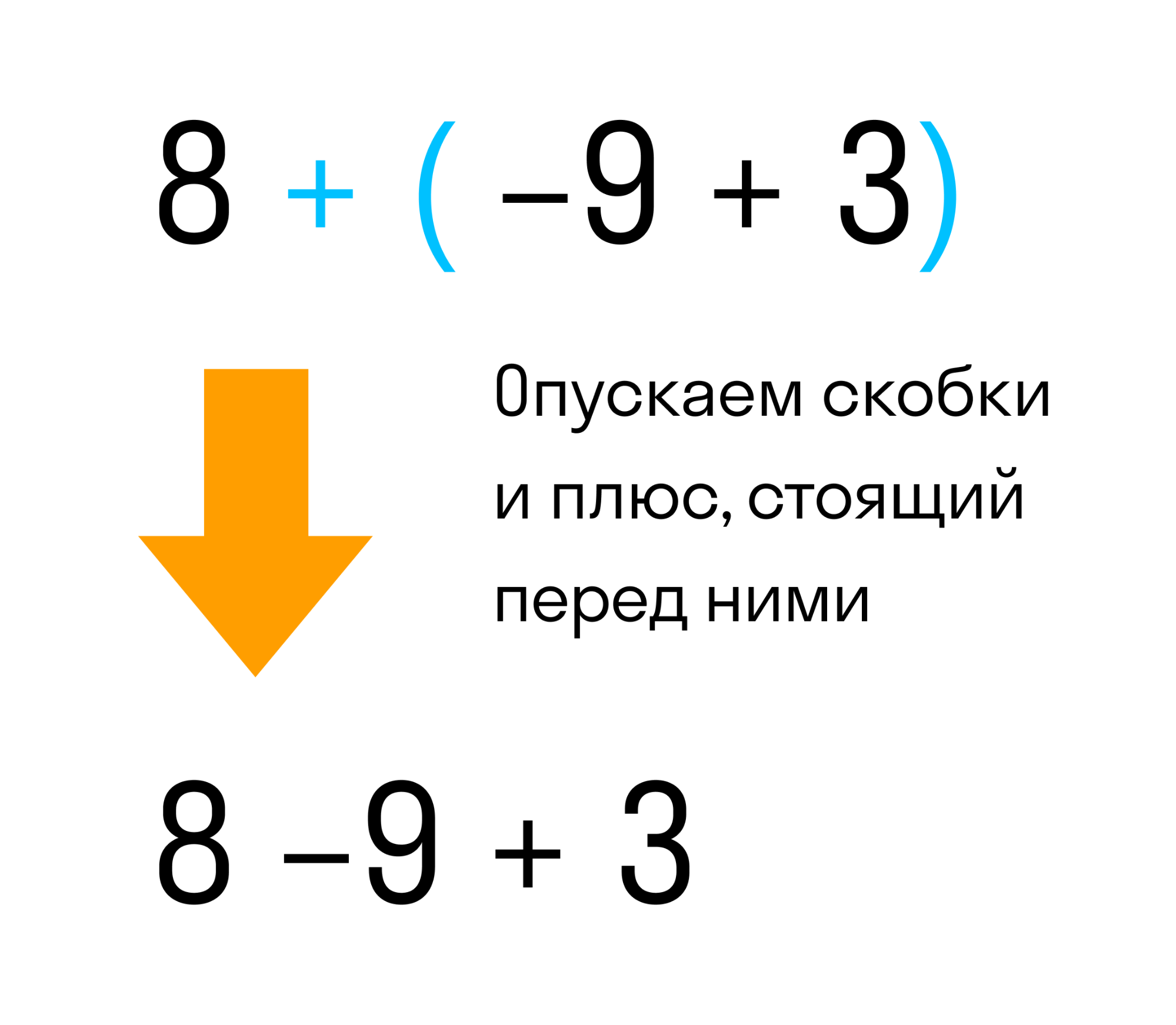
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

• 8 + (−9 + 3) = 2
• 8 − 9 + 3 = 2

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

• 8 + (−9 + 3) = 8 − 9 + 3
• 2 = 2

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Как рассуждаем:

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

8 + (−3 − 1) = 8 − 3 − 1

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Как рассуждаем:

Перед скобками стоит плюс, значит применим то же правило:

6 + (−2) = 6 − 2

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

3a + (−4b) = 3a − 4b

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

2 + (−3 + 1) + 3 + (−6)

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

Как рассуждаем:

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

6 + (−3) + (−2) = 6 − 3 − 2

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении (−7)

Как рассуждаем:

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

(−7) = −7

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Как рассуждаем:

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

9a + (−5b + 6c) + 2a + (−2d) = 5a −5b + 6c + 2a − 2d

Пример 2: умножаем ячейку на число

В данном случае принцип тот же, что и в разобранном выше примере. Разница заключается лишь в том, что перемножать мы будем не два конкретных числа, а одно число и ячейку, в которой содержится числовое значение.

Допустим, у нас есть таблица, в которой представлена стоимость одной единицы товара. Нам нужно посчитать стоимость при количестве 5 шт.

1. Встаем в ячейку, в которой требуется выполнить умножение (в нашем случае – это самая верхняя ячейка столбца C, не считая шапки таблицы). Затем:
   • ставим знак “=”;
   • указываем адрес ячейки – первого числа (для нас – это B2). Сделать это можно путем ручного ввода координат с клавиатуры. Также можно просто кликнуть по нужной ячейке в самой таблице;
   • пишем знак умножения “*“;
   • указываем число 5.
2.  Нажимаем Enter, чтобы получить результат.

Примеры умножения чисел с разными знаками

Пример 1

Необходимо выполнить умножение отрицательного числа -5 на положительное число 8.

Решение

Согласно правилу умножения чисел с различными знаками, перемножим модули заданных множителей.

|-5|= 5 и |8| = 8, тогда перемножение натуральных чисел 5 и 8 даст в результате число 40.

Присвоим данному результату знак минус, получим: -40

Кратко решение можно записать так: (-5)·8 =-(5·8) =-40.

Ответ: (-5)·8 =-40.

Пример 2

Необходимо произвести умножение чисел ,(2) и -214.

Решение

Первым шагом переведем периодическую десятичную дробь в обыкновенную (первый множитель), затем выполним переход от смешанного числа к неправильной дроби (второй множитель), применим далее правило умножения чисел с разными знаками и тогда получим: ,2·-214= 29·-94= -29 ·94= -12 

Ответ: ,2·-214=-12.

Отдельно приведем пример умножения чисел с разными знаками, когда один из множителей или оба – иррациональные числа, которые записаны в виде корней, логарифмов и пр. В таких случаях ответ зачастую представляется в виде числового выражения.

Пример 3

Необходимо выполнить умножение sin3 на -1,3.

Решение

Используем правило умножения чисел с разными знаками, чтобы преобразовать равенство: sin3·(-1,3) =-(1,3·sin3).

Никак более упростить выражение мы не сможем, оно и будет являться ответом.

Ответ: sin3·(-1,3)=-(1,3·sin3).

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Общие сведения о знаках в Excel

В программе предусмотрены различные символы в зависимости от ситуации. Например, это могут быть знаки математических операций:

• Знак равенства («=»);
• Знаки больше и меньше;
• Комбинация знаков больше и меньше со знаком равенства;
• Умножение и деление;
• Сложение и вычитание;
• Знак корня и возведения в степень;
• Знак модуля;

Общие сведения о формулах есть здесь.

Помимо символов математических операций, также часто используется знак доллара. И наконец стоит упомянуть о различных спецсимволах, которые к формулам и вычислениям не относятся, а используются просто в тексте.

Ниже рассмотрены те случаи, которые мы раньше не рассматривали. Для остальных ситуаций со знаками и заменяющими их операциями переходите по указанным выше ссылкам.

Ставим знак умножения в Microsoft Word

Сегодня мы рассмотрим способы, которые позволят поставить в Microsoft Word знак умножения.

Способ 1: набор знака умножения в виде точки с клавиатуры

Самый простой и доступный способ выставления знака умножения в тексте, который используется в большинстве случаев. Для этого вам потребуется нажать на клавиатуре сочетание клавиш Shift+8, после чего нужный знак отобразится на экране.

Способ 2: набор знака умножения в виде креста с клавиатуры

В ряде случаев пользователю может потребоваться поставить иную вариацию знака умножения, а именно, в виде креста. Сразу следует отметить, что такой вариант не используется для вычислительных формул, а лишь для красивой визуальной составляющей.

В данном случае вам потребуется набрать букву «х» в русской или английской раскладке клавиатуры.

Способ 3: вставка знака умножения через меню Word

В Microsoft Word имеется встроенный набор символов, которые вы в любой момент можете использовать, если у вас нет возможности обратить к клавиатуре.

1. Для этого щелкните по кнопке

«Вставка» и в отобразившемся меню выберите пункт «Символ».

На экране отобразится меню символов, среди которых вам следует найти букву «x» или символ «*», выделить его одним кликом мыши, а затем добавить в буфер обмена сочетанием клавиш Ctrl+C.

Вам остается вставить символ в текст сочетанием клавиш Ctrl+V.

Способ 4: через меню символов в Windows

Найти необходимый символ умножения вы можете и через специальную утилиту Windows, которая установлена на компьютер по умолчанию.

1. Откройте строку поиска и пропишите в нее запрос

«Таблица символов». Откройте появившийся результат.

Опять же, на экране откроется окно символов, в котором вам следует найти или букву «x», или символ «*», только первый лишь визуально имитирует знак умножения, а второй им и является.

Дважды кликните по выбранному символу, чтобы он отобразится в нижней части окна. Он автоматически будет помещен в буфер обмена. Теперь вы можете вставить его в текстовый документ сочетанием клавиш Ctrl+V.

Добавление знака умножения в виде точки

Вы, наверное, знаете о том, что в Ворде имеется довольно большой набор неклавиатурных знаков и символов, которые во многих случаях могут оказаться очень полезными. Мы уже писали об особенностях работы с этим разделом программы, и знак умножения в виде точки мы тоже будем искать там.

Вставка знака через меню “Символ”

1. Кликните в том месте документа, где нужно поставить знак умножения в виде точки, и перейдите во вкладку “Вставка”.

2. Откройте диалоговое окно “Символ”. Для этого в группе “Символы” нажмите кнопку “Символ”, а затем выберите пункт “Другие символы”.

3. В выпадающем меню “Набор” выберите пункт “Математические операторы”.

4. В изменившемся списке символов найдите знак умножения в виде точки, кликните по нему и нажмите “Вставить”. Закройте окно.

5. Знак умножения в виде точки будет добавлен в указанном вами месте.

Вставка знака с помощью кода

У каждого знака, представленного в окне “Символ”, есть свой код. Собственно, именно в этом диалоговом окне и можно подсмотреть, какой код имеет знак умножения в виде точки. Там же вы сможете увидеть комбинацию клавиш, которая поможет преобразовать введенный код в знак.

1. Установите указатель курсора в том месте, где должен находиться знак умножения в виде точки.

2. Введите код “2219” без кавычек. Делать это нужно на цифровом блоке клавиатуры (расположен справа), предварительно убедившись в том, что режим NumLock активен.

3. Нажмите “ALT+X”.

4. Введенные вами цифры будут заменены на знак умножения в виде точки.

Пример 6: умножаем столбец на ячейку

Предположим, нам нужно посчитать скидку по перечню товаров, представленному в одном столбце (B). Размер скидки указан в отдельной ячейке (E2).

Алгоритм действий следующий:

1. Для начала пишем в самой верхней ячейке столбца C (не считая шапки) формулу умножения ячейки B2 на E2.
2. Не спешим нажимать клавишу Enter. Дело в том, что сейчас в формуле используются относительные ссылки, а это значит, что при ее копировании в другие ячейки произойдет смещение адресов (т.е. B3 будет умножаться на E3). Нам же нужно зафиксировать адрес E2, т.е. сделать ссылку на эту ячейку абсолютной. Для этого находясь курсором до, после, или внутри адреса (между буквой и цифрой) нажимаем клавишу F4.
3. Перед обозначением столбца и номером строки появятся символы “$”. Теперь можно нажимать Enter.
4. Растягиваем формулу на другие ячейки с помощью маркера заполнения.
5. Как мы можем убедиться на примере формулы в ячейке C9, в ней по-прежнему участвует ячейка E2, а это значит, что мы все сделали правильно.

Пример 1: умножаем число на число

Самый простой пример – это произведение двух конкретных чисел. В данном случае Эксель выступает в роли обычного калькулятора.

1. Встаем в любую свободную ячейку, затем:
   • ставим в ячейке (или в строке формул) знак “=”;
   • пишем первое число (множимое;
   • ставим знак умножения – “*“;
   • указываем второе число (множитель).
2. После нажатия клавиши Enter получаем результат в ячейке с формулой.

Примечание: при работе с вычислениями нужно помнить, что в Excel действуют такие же законы приоритета, что и в обычной арифметике, т.е. сперва выполняется умножение или деление, и только потом – сложение или вычитание.

В отличие от того, как записываются выражения со скобками на бумаге, в программе всегда ставится знак умножения (и до, и после скобок). Допустим, у нас есть вот такое выражение: .

В ячейке нам нужно написать следующую формулу: .

Нажав Enter получаем ответ.

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1/x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Ставим знак умножения в Microsoft Word

Сегодня мы рассмотрим способы, которые позволят поставить в Microsoft Word знак умножения.

Способ 1: набор знака умножения в виде точки с клавиатуры

Самый простой и доступный способ выставления знака умножения в тексте, который используется в большинстве случаев. Для этого вам потребуется нажать на клавиатуре сочетание клавиш Shift+8, после чего нужный знак отобразится на экране.

Способ 2: набор знака умножения в виде креста с клавиатуры

В ряде случаев пользователю может потребоваться поставить иную вариацию знака умножения, а именно, в виде креста. Сразу следует отметить, что такой вариант не используется для вычислительных формул, а лишь для красивой визуальной составляющей.

В данном случае вам потребуется набрать букву «х» в русской или английской раскладке клавиатуры.

Способ 3: вставка знака умножения через меню Word

В Microsoft Word имеется встроенный набор символов, которые вы в любой момент можете использовать, если у вас нет возможности обратить к клавиатуре.

1. Для этого щелкните по кнопке

«Вставка» и в отобразившемся меню выберите пункт «Символ».

На экране отобразится меню символов, среди которых вам следует найти букву «x» или символ «*», выделить его одним кликом мыши, а затем добавить в буфер обмена сочетанием клавиш Ctrl+C.

Вам остается вставить символ в текст сочетанием клавиш Ctrl+V.

Способ 4: через меню символов в Windows

Найти необходимый символ умножения вы можете и через специальную утилиту Windows, которая установлена на компьютер по умолчанию.

1. Откройте строку поиска и пропишите в нее запрос

«Таблица символов». Откройте появившийся результат.

Опять же, на экране откроется окно символов, в котором вам следует найти или букву «x», или символ «*», только первый лишь визуально имитирует знак умножения, а второй им и является.

Дважды кликните по выбранному символу, чтобы он отобразится в нижней части окна. Он автоматически будет помещен в буфер обмена. Теперь вы можете вставить его в текстовый документ сочетанием клавиш Ctrl+V.