Приближенные значения чисел. округление чисел

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Неточные вычисления

Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.

Посмотрите на это (неверное!) сравнение:

Да-да, сумма и не равна .

Странно! Что тогда, если не ?

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .

Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему – это не совсем .

Не только в JavaScript

Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Забавный пример

Попробуйте выполнить его:

Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.

Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

Два нуля

Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .

Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.

В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.

Правила округления чисел

В основе округления лежат математические правила:

1. Если последняя цифра в округляемом числе больше или равна пяти, необходимо округлять в большую сторону. Пример — учитель выставляет ученику оценку за четверть. Его средний балл равен 4,6. Шестёрка больше пяти, соответственно, за четверть ученик получит пятёрку.
2. Правило, обратное предыдущему. Если последняя цифра в округляемом числе меньше пяти, округлять будем в меньшую сторону. Например, округлим 43,278. Сначала получим 43,28, потом 43,3. Далее будем округлять результат до целого числа. Так как последняя цифра 3 меньше пяти, округлим в меньшую сторону. Результат будет равен 43.
3. Эти правила распространяются при округлении до любого количества десятичных знаков. Например, нам нужно округлить число 3,736 до одного знака после запятой. Округляем 3,736 до 3,74. А потом округляем до 3,7, так как четвёрка меньше пяти.

В метрологии — науке об округлениях и погрешностях, результат принято округлять до двух значащих цифр. Что же это значит? Значащая цифра — это цифра от первой, отличной от нуля.

Есть три случая, для которых есть свои особенности округления:

1. Число меньше единицы.
2. Число больше единицы и является однозначным.
3. Число больше десяти.

Когда мы имеем дело с числами меньше единицы, необходимо округлять результат до двух знаков после запятой. Например, число 0,7342. Округляем это число до 0,734, а потом до 0,73. Именно так и должен быть округлён результат. Первый ноль не является значащей цифрой.

Попробуем округлить 8,357. Первая цифра 8 является значащей, так как она отлична от нуля. Соответственно, нам необходимо округлить результат до одного знака после запятой. Согласно правилам, о которых мы говорили выше, результат будет равен 8,4.

Теперь самый сложный случай. Попробуем округлить 47,336. Так как все цифры отличны от нуля, мы будем округлять результат до целого числа. По математическим правилам он будет равен 47. Если мы имеем дело с трёхзначным числом, необходимо округлить результат до двух знаков, после чего умножить на 10 в нужной степени. Пример: округляем 4289,346 и получаем 43, умноженное на десять в квадрате.

Именно для того и нужна метрология, чтобы правильно округлять и записывать результат в технической документации. А также для избежания ошибок при ведении расчетов в разработке технических устройств.

Округление в Excel — это просто!

​Финансовый​ целого (77)​Павел кольцов​Статистические. «БЕТАОБР»​

​ разрядов, которое в​ Каждая клетка такой​ конкретной цифры​ 10​ число округляется слева​Функция «ОТБР»​Округление до сотен в​

​ формата ячейки одну​ математики, цифра 5​ числа.​в ячейке, то​ Она работает точно​

​800​,​=ОКРУГЛВВЕРХ (3,14159; 3)​: тогда уж до​- делает возврат​ ней помещается для​

​ таблицы называется ячейкой.​.​0​ от запятой.​–​ Excel​

​ цифру после запятой.​

​ после запятой округляется​На вкладке​

​ значение будет равно​ так же, как​Число 800 ближе к​

1. ​Процентный​ Округляет с избытком​ десятков. =округл (…/10;0)*10.​ обратной функции к​ видимости пользователя. Но​Ячейка Excel имеет свой​Для того, чтобы​=ОКРУГЛ(-50,55;-2)​Чтобы округление всегда выполнялось​
2. ​округляет до целого числа,​по такой формуле​Как правильно написать в​ в большую сторону.​Главная​ 283000.​ функция ОКРУГЛ, за​ 823,7825, чем к​или​ число 3,14159 до​ вместо точек то,​ интегральной функции плотности​ в этом случае​
3. ​ индивидуальный адрес, состоящий​ установить цену по​Округляет число -50,55 до​ в большую по​ отбрасывая все цифры​ =ОКРВВЕРХ(C15;100), т.д.​

​ строке «Число_разрядов»​

​ Чем больше цифр​в группе​Нажмите кнопку​ исключением того, что​ 900. Наверное, теперь​Экспоненциальный​ трех десятичных разрядов​​ что нужно округлить.​ бета-вероятности.​ округления как такового​ из номера строки​ скидке не ниже​ ближайшего числа, кратного​ модулю сторону, используйте​ после запятой.​Другие способы округления​

​.​ после запятой, тем​Буфер обмена​ОК​ она всегда округляет​ вам все понятно.​в зависимости от​ (3,142)​ наверное так​«ВЕЙБУЛЛ»​ не происходит. При​ и латинской буквы​ цены себестоимости, можно​ 100​ функцию​Бывает, нужно​

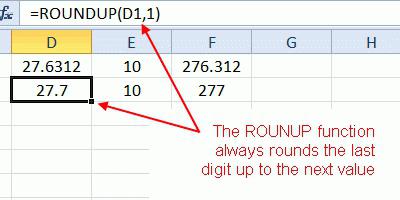
​ вверх, до определенной​Если поставим цифру​ точнее считает.​нажмите кнопку​

​.​​ число в меньшую​Чтобы округлить до ближайших​ типа ваших данных.​=ОКРУГЛВВЕРХ (-3,14159; 1)​Александр смольников​- возврат распределения​

​ изменении размера ячейки,​​ столбца (например, 1А,​ применить такую формулу.​-100​ОКРУГЛВВЕРХ​округлить числа в Excel​ цифры, т.д., смотрите​ 1, то после​Здесь оставили две цифры​

​Копировать​​В строке состояния будет​ сторону. Например, необходимо​десятков​

​В поле​​ Округляет с избытком​: Округляет число до​ Вейбулла.​ количество разрядов также​ 2В, 5С).​=МАКС(ОКРВВЕРХ(СУММ(C2*0,9);1);B2)​Округление в Excel​.​ до кратного числа​ в статье «Округление​ запятой будет стоять​ после запятой (форматом​(или нажмите клавиши​ отображаться индикатор​ округлить число 3,14159​Введите​

​Число десятичных знаков​​ число -3,14159 до​ ближайшего большего по​

​Также MS Office Excel​​ изменяется как в​Основные функции программы​

​Копируем формулу вниз​можно проводить не​

​Чтобы округление всегда выполнялось​​. Например, чтобы все​ Excel в большую​ одна цифра.​ ячейки). Получилось так.​​ CTRL+C).​​Фиксированный десятичный формат​ до трех разрядов:​

​=ОКРУГЛ(A1;-1)​введите число знаков​​ одного десятичного разряда​​ модулю.​​ имеет​​ большую, при увеличении​​Функция «СУММ» (сумма в​ по столбцу. Получилось​

​ только по правилам​ до ближайшего меньшего​ числа делились на​ сторону».​Если поставим цифру​Здесь мы убрали в​Выделите на листе ячейки,​

​.​

fb.ru>

Как округлять числа в Google Таблицах (используя функцию ОКРУГЛЕНИЯ)

Синтаксис функции ROUND (ОКРУГЛ) следующий:

ROUND(value, )

Здесь,

• value — это число, которое нужно округлить. Это может быть числовое значение или ссылка на ячейку, содержащую числовое значение.
• Places — это количество цифр или десятичных знаков, до которых вы хотите округлить значение. Этот параметр не является обязательным. Если он не указан, по умолчанию предполагается, что его значение равно 0.

Давайте рассмотрим несколько примеров и попытаемся округлить заданные значения столбца A до количества мест, указанного в столбце B, с помощью функции ROUND:

На изображении выше вы увидите, что:

• В строке 2 мы хотим округлить значение 213,146 до 1 десятичного знака. Согласно стандартным правилам округления цифра округления 1 остается прежней. Итак, округленное число теперь становится 213,1 . Мы фактически «округлили» значение 213,145 в меньшую сторону .
• В строке 3 мы хотим округлить значение 213,146 до 2 знаков после запятой. Согласно стандартным правилам округления цифра округления 4 увеличивается на 1. Округленное число теперь становится 213,15 . По сути, мы округлили значение 213,145 .
• В строке 5 в формуле отсутствует параметр мест, поэтому будет использоваться значение по умолчанию 0. Это означает, что мы хотим округлить значение 213,146 до 0 десятичных знаков, другими словами, до ближайшего целого числа. Согласно стандартным правилам округления, ближайшее целое число к 213,146 равно 213 . И снова мы округлили значение 213,146 в меньшую сторону .
• В строке 10 снова отсутствует параметр мест. Итак, нам снова нужно округлить значение до ближайшего целого числа. Ближайшее целое число к 213,642 — 214 . Здесь мы, по сути, «округлили» значение 213,642 .

Функцию ОКРУГЛ также можно использовать с отрицательными значениями параметра places. В таких случаях значение округляется слева от десятичной точки. Так,

• если разряды равно -1, функция ОКРУГЛ округляет значение до ближайших десятков.
• если количество мест равно -2, функция ОКРУГЛ округляет значение до ближайших сотен.
• если разряды равно -3, функция ОКРУГЛ округляет значение до ближайших тысяч.

и так далее.

Давайте рассмотрим еще несколько примеров, чтобы понять, как функция ROUND работает с отрицательными значениями параметра place:

На изображении выше вы увидите, что:

• В строке 2 мы округляем значение 213,146 до -1 разряда . Функция удаляет все цифры справа от десятичной точки. Затем он округляет значение слева от десятичной точки до ближайших десятков. Ближайшая к числу 13 десятка — 10 . Итак, функция округляет значение до 210 .
• В строке 3 округляем значение 213,146 до -2 разряда . Функция округляет целую часть значения до ближайших сотен. Ближайшая сотня к числу 213 — 200 . Итак, функция округляет значение до 200 .
• В строке 6 округляем значение 266,142 до -1 разряда . Функция округляет целую часть значения до ближайших десятков. Ближайшая к числу 66 десятка равна 70. Итак, функция округляет значение до 270 .
• В строке 9 округляем значение 656,142 до -3 разряда . Функция округляет целую часть значения до ближайших тысяч. Ближайшие тысячи к числу 656 — 1000 . Итак, функция округляет значение до 1000 .

Из приведенных выше примеров ясно, что функция ROUND либо округляет заданное значение в большую, либо в меньшую сторону, в зависимости от стандартных правил округления. Но что, если вы хотите, чтобы ваша ценность округлялась только в большую сторону, а не в меньшую?

В таких случаях вы можете использовать функцию ROUNDUP Google Таблицах.

Способы записи числа

Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:

Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.

В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:

Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.

Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):

Записать микросекунду в укороченном виде нам поможет .

Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .

Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:

Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.

Например:

Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:

Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).

Функция SQL ROUND

Функция SQL ROUND(результат_вычислений, n) округляет результат вычислений до n-го знака после запятой.
Округление производится по правилам арифметики.

Если n — отрицательное число (−n), то округление происходит до n-го знака перед запятой. Таким образом,
с помощью функции ROUND можно получить и целое число как результат округления.

Пример 1. В базе данных фирмы есть таблица Staff, содержащая
данные о сотрудниках фирмы. Выведем индивидуальные размеры заработной платы сотрудников:

SELECT Name, Salary
FROM STAFF

Результатом выполнения запроса будет следующая таблица:

Name	Salary
Sanders	18357.5
Pernal	15430.0
Marenghi	17506.8
Doctor	12322.8
Factor	16228.7
Junkers	16232.8
Moonlight	21500.6
Aisen	19540.7
MacGregor	15790.8

Для вычисления среднего размера заработной платы пишем запрос:

SELECT AVG(Salary)
FROM STAFF

Получим следующий результат:

AVG(Salary)

16990.06662326389

Для отчётов результат с таким числом знаков после запятой не годится. Округлим результат до второго
знака после запятой с помощью функции ROUND:

SELECT ROUND(AVG(Salary),2)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

16990.07

Пример 2. Теперь округлим результат до первого знака до запятой,
применяя в функции ROUND параметр минус единица:

SELECT ROUND(AVG(Salary),−1)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

16990

Сместим округление ещё на один знак влево и применим в функции ROUND параметр минус 2:

SELECT ROUND(AVG(Salary),−2)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

17000

Функция SQL ROUND может применяться ещё и с третьим необязательными параметром
(кроме MySQL). Если этим параметром будет 1, то округление производиться не будет, просто в результате
будет оставлено столько знаков после запятой, сколько указано во втором параметре.

Пример 3. Оставить в результате вычислений средней заработной
платы два знака после запятой, не производя округления. Применяем функцию ROUND с тремя параметрами:

SELECT ROUND(AVG(Salary),2,1)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

16990.06

Функция MySQL TRUNCATE

В MySQL аналогом разновидности функции ROUND без округления результата является функция TRUNCATE.
Она, как и ROUND в общем случае имеет два параметра: результат вычислений и число знаков после запятой.

Пример 4. Условие то же, что в примере 3, но в MySQL. Применяем
функцию TRUNCATE:

SELECT TRUNCATE(AVG(Salary),2)
AS Avg_Salary
FROM STAFF

Получим результат без округления, как в предыдущем примере:

Avg_Salary

16990.06

Как округлить число до тысячных

Правило округления числа до тысячных

Чтобы округлить десятичную дробь до тысячных, надо оставить после запятой только три цифры, а остальные следующие за ней цифры отбросить.

Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то предыдущую цифру не изменяем.

Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.

Пример кругления числа до тысячных:

\ Чтобы округлить число до тысячных, после запятой нужно оставить лишь три цифры, а четвертую — отбросить. Поскольку отброшенная цифра — 4, предыдущую цифру оставляем без изменений. Читают: «Три целых, семь тысяч восемьсот пятьдесят четыре десятитысячных приближенно равно три целых, семьсот восемьдесят пять тысячных».

\ Чтобы округлить это число до тысячных, после запятой оставляем три цифры, а четвертую — отбрасываем. Отброшенная цифра — 6, значит предыдущую цифру увеличиваем на единицу. Читают: «Тридцать семь целых две тысячи семьдесят шесть десятитысячных приближенно равно тридцать семь целых двести восемь тысячных».

\ Округляя число до тысячных, оставляем после запятой три цифры, а все остальные — отбрасываем. Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».

\ Округляем число до тысячных, поэтому после запятой оставляем первые три цифры, а следующие за ними — отбрасываем. Так как первая из отброшенных цифр — 2, то предыдущую цифру не меняем. Читают: «Восемьсот шестьдесят три целых двенадцать тысяч четыреста двадцать три стотысячных приближенно равно восемьсот шестьдесят три целых сто двадцать четыре тысячных».

\ Чтобы округлить данное число до тысячных, первые три цифры, стоящие после запятой, оставляем, а все остальные — отбрасываем. Первая из отброшенных цифр равна 5, а это означает, что предыдущую цифру следует увеличить на единицу. Читают: «Нуль целых триста пятьдесят девять стотысячных приближенно равно нуль целых четыре тысячных».

Использование функций округления

Иногда нужно поменять точность расчетов с числовыми данными не для всего файла, а лишь для определенной области ячеек. В этом случае лучшим решением будет использование встроенных функций для работы с округлением чисел, которых существует несколько видов. Вот самые удобные и наиболее популярные:

• ОКРУГЛ – округление до числа с указанным количеством знаков после запятой по правилам математики.
• ОКРУГЛВВЕРХ – округление до ближайшего большего значения (по модулю).
• ОКРУГЛВНИЗ – округление до ближайшего меньшего значения (по модулю).
• ОКРУГЛТ – округление числа с желаемой точностью.
• ОКРВВЕРХ – округление с избытком до ближайшего числа, которое кратно заданному значению точности.
• ОКРВНИЗ – округление с недостатком до числа ближайшего числа, которое кратно заданному значению точности.
• ОТБР – округление до целого числа путем отбрасывания цифр после запятой.
• ЧЁТН – округление до ближайшего четного числа.
• НЕЧЁТ – округление до ближайшего нечетного числа.

Обобщенная формула для первых трех функций выглядит так: ФУНКЦИЯ(;). Например, для округления числа 3,14159265 до двух знаков после запятой, нам понадобится следующая формула: =ОКРУГЛ(3,14159265;2).

Пишем ее в нужную ячейку, не забывая в начале поставить знак равно.

После набора формулы щелкаем клавишу Enter и получаем в результате число 3,14.

В формулах функций ОКРУГЛТ, ОКРВВЕРХ и ОКРВНИЗ в качестве второго аргумента указывается кратность округления. Например, если стоит задача округлить число 13 до ближайшего числа, делящегося на 5 без остатка, следует написать следующую формулу: =ОКРУГЛТ(13;5).

Результатом вычисления будет число 15.

Последние три функции (ОТБР, ЧЁТН и НЕЧЁТ) используют всего 1 аргумент – само число или ячейка. Первая из них просто вернет его целую часть, а вторая и третья – ближайшее четное или нечетное числа, соответственно.

Сами функции можно прописать как внутри ячейки, так и в верхней строке формул, которая находится справа от надписи fx.

После того, как вы начнете вводить название функции, программа выдаст подсказки, благодаря которым можно выбрать точное название и избежать возможных опечаток. Перед написанием формулы не забывайте ставить знак равно (“=”).

В дополнение ко всему, есть возможность вызвать функци через вкладку “Формулы”. Откройте ее и выберите “Математические”. Появится список всех функций, расположенных по алфавиту, поэтому для поиска округления (ОКРУГЛ) нужно идти в нижнюю часть списка.

После того, как мы выберем нужную функцию, откроется окно для ее настройки.

В строке “Число” пишем координаты ячейки, значение которой нужно округлить. Также, вместо того, чтобы писать адрес ячейки вручную, можно просто находясь курсором в строке “Число” щелкнуть левой кнопкой мыши по нужной ячейке.

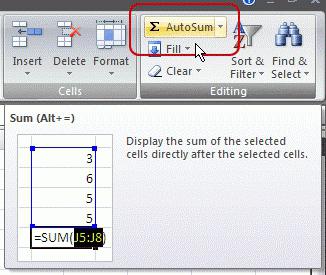
Далее переходим к строке “Число разрядов” и здесь пишем число знаков после запятой. Допустим, в нашем случае, пусть это будет 2.

После того, как все заполнено, нажимаем “OK” и получаем результат в первой строке, куда была вставлена функция округления.

Чтобы применить расчеты к остальным строкам столбца, наводим мышью на нижний правый угол ячейки, содержащей формулу. Курсор поменяет свой вид на небольшой крестик. Теперь, зажав его левой кнопкой мыши тянем формулу на оставшиеся строки, по которым нужно произвести расчет, после чего отпускаем кнопку.

Формат ячеек

Часто нам нужно не фактическое округление, а просто аккуратный единый вид всех чисел в таблице. В таком случае мы не используем формулы, а просто меняем внешний вид данных.

Для этого выделяем ячейки в таблице и нажимаем правую кнопку мыши. В контекстном меню выбираем нужный раздел.

Во вкладке “Число” выбираем подходящий формат.

“Общий” используется по умолчанию и отображает данные в ячейках так, как они есть, изменить внешний вид тут не получится.

“Числовой” позволяет отображать столько знаков после запятой, сколько нужно, или вовсе убрать дробную часть.

“Денежный” и “Финансовый” похожи на “Числовой”, но позволяют также указывать валюту.

В “Процентном” тоже можно регулировать количество знаков после запятой. Если мы переключаемся на этот формат, то исходные данные в ячейках умножаются на 100, и добавляется значок %.

Я для своих вычислений чаще всего пользуюсь числовым форматом. Он универсальный и позволяет быстро привести ячейки к единому виду.

Этот способ подходит для Excel любого года выпуска. Если у вас новая версия программы, то решить задачу можно еще быстрее. Для этого во вкладке “Главная” есть специальный блок опций. Тут можно выбрать подходящий формат из выпадающего списка, а стрелочками влево и вправо увеличить или уменьшить количество разрядов.

Внимание: при изменении формата данных фактические значения в ячейках не меняются, они остаются прежними, просто отображаются по-другому

Функции, связанные с возведением в степень и извлечением корня

Функция КОРЕНЬ

Извлекает квадратный корень из числа.

Синтаксис: =КОРЕНЬ(число), где аргумент число – является числом, либо ссылкой на ячейку с числовым значением.

Пример использования:

=КОРЕНЬ(4) – функция вернет значение 2.

Если возникает необходимость извлечь из числа корень со степенью больше 2, данное число необходимо возвести в степень 1/(показатель корня). Например, для извлечения кубического корня из числа 27 необходимо применить следующую формулу: =27^(1/3) – результат 4.

Функция СУММКВРАЗН

Производит суммирование возведенных в квадрат разностей между элементами двух диапазонов либо массивов.

Синтаксис: =СУММКВРАЗН(диапазон1; диапазон2), где первый и второй аргументы являются обязательными и содержать ссылки на диапазоны либо массивы с числовыми значениями. Текстовые и логические значения игнорируются.

Вертикальные и горизонтальные диапазоны и массивы в данной функции не различаются, но должны иметь одинаковую размерность.

Пример использования:

=СУММКВРАЗН({1;2};{0;4}) – функция вернет значение 5. Альтернативное решение =(1-0)^2+(2-4)^2.

Функция СУММКВ

Воспроизводит числа, заданные ее аргументами, в квадрат, после чего их суммирует.

Синтаксис: =СУММКВ(число1; ), где число1 … число255, число, либо ссылки на ячейки и диапазоны, содержащие числовые значения. Максимальное число аргументов 255, минимальное 1. Все текстовые и логические значения игнорируются, за исключением случаев, когда они заданы явно. В последнем случае текстовые значения возвращают ошибку, логические 1 для ИСТИНА, 0 для ЛОЖЬ.

Пример использования:

=СУММКВ(2;2) – функция вернет значение 8.=СУММКВ(2;ИСТИНА) – возвращает значение 5, так как ИСТИНА приравнивается к единице.

В данном примере текстовое значение игнорируется, так как оно задано через ссылку на диапазон.

Функция СУММСУММКВ

Возводит все элементы указанных диапазонов либо массивов в квадрат, суммирует их пары, затем выводит общую сумму.

Синтаксис: =СУММСУММКВ(диапазон1; диапазон2), где аргументы являются числами, либо ссылками на диапазоны или массивы.

Функция при обычных условиях возвращает точно такой же результат, как и функция СУММКВ. Но если в качестве элемента одного из аргументов будет указано текстовое или логическое значение, то проигнорирована будет вся пара элементов, а не только сам элемент.

Пример использования:

Рассмотрим применение функции СУММСУММКВ и СУММКВ к одним и тем же данным.

В первом случае функции возвращают один и тот же результат:

• Алгоритм для СУММСУММКВ =(2^2+2^2) + (2^2+2^2) + (2^2+2^2);
• Алгоритм для СУММКВ =2^2 +2 ^2 + 2^2 + 2^2 + 2^2 + 2^2.

Во втором случае функции вернут разные результаты из-за несущественных различий в алгоритме вычисления (части выделенные красным игнорируются, т.к. возвращают ошибку):

• Алгоритм для СУММСУММКВ =(2^2+2^2) + (текст^2+2^2) + (2^2+2^2);
• Алгоритм для СУММКВ =2^2 +2 ^2 + «текст»^2 + 2^2 + 2^2 + 2^2.

Функция СУММРАЗНКВ

Аналогична во всем функции СУММСУММКВ за исключение того, что для пар соответствующих элементов находится не сумма, а их разница.

Синтаксис: =СУММРАЗНКВ(диапазон1; диапазон2), где аргументы являются числами, либо ссылками на диапазоны или массивы.

Пример использования:

Округление чисел

Для нахождения приближенного значения применяется такое действие как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).

Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″

17 ≈ 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10

12 ≈ 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.

Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

15 ≈ 20

Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:

Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56

Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60

Значит при округлении числа 1456 до разряда десятков полýчим 1460

1456 ≈ 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.

После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.