Калькулятор комплексных чисел. вычисление выражений с комплексными числами

Сопряженные числа и их свойства

Пусть —
комплексное число. Число ,
отличающееся от числа лишь знаком
при мнимой части, называется числом, сопряжённым с .

Свойства сопряжённых чисел

1) (число,
сопряжённое сопряжённому числу, равно данному числу);

2) если и —
комплексные числа, то и
(число, сопряжённое
с суммой двух чисел, равно сумме чисел, сопряжённых со слагаемыми и число, сопряжённое с
произведением, равно произведению чисел, сопряжённых с сомножителями).

3) если ,
то и
— положительное
действительное число, равное нулю тогда и только тогда, когда ,
т. е. когда и
.

Пример 8. Даны комплексные числа
и
. Убедиться
в справедливости свойств сопряжённых чисел.

Решение. Сопряжёнными данным комплексным числам являются числа
и . Сумма данных комплексных чисел:

,

а произведение:

.

В свою очередь

,

Таким образом, справедливость свойств сопряжённых чисел доказана.

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа:
• Получение мнимой части числа:
• Модуль числа:
• Аргумент числа:
• Экспонента:
• Логарифм:
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(42 + (-3)2) = √25 = 5

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби (, , ), десятичные дроби (, , ), а также числа в экспоненциальной форме (, ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (, , , ) для перемещения по элементам

Изображение комплексных чисел радиус-векторами координатной плоскости

      Рассмотрим плоскость с заданной на ней   Oxy   и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

      Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число   z = x + i y   радиус–вектором с координатами   (x , y).

      Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.

      При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Алгебраическая форма записи комплексных чисел

      Пусть x и y — произвольные вещественные числа.

      Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

      Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0).

      Комплексные числа, заданные парами (0, y), называют чисто мнимыми числами.

      Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи.

      Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число   z, заданное парой вещественных чисел   (x, y), записывается в виде

z = x + i y .

(1)

где использован символ   i , называемый мнимой единицей.

      Число x называют вещественной (реальной) частью комплексного числа   z = x + i y   и обозначают   Re z.

      Число y называют мнимой частью комплексного числа   z = x + i y   и обозначают   Im z.

      Комплексные числа, у которых   Im z = 0 , являются вещественными числами.

      Комплексные числа, у которых     Re z = 0 , являются чисто мнимыми числами.

      Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Деление комплексных чисел

Давайте разделим (3+2i)/(1–4i)

В этот момент вы можете подумать, что можете просто разделить действительные и мнимые части… но не так быстро.

Как и в алгебре, мы должны разделить оба члена числителя на знаменатель, что оставляет нас с той же проблемой:

Что на
самом деле означает деление на комплексное число?

По правде говоря, это сбивает с толку. Разве не было бы хорошо, если бы мы могли избавиться от комплексного числа в знаменателе?

Хорошие
новости → Именно это мы и собираемся сделать!

Сопряжённые числа

Ключом к решению этой
проблемы является выяснение того, как преобразовать знаменатель в вещественное
число.

Самый простой способ
сделать это — использовать комплексное
сопряжение.

Комплексно-сопряжённое число какому-то числу это тоже самое число только с другим знаком возле мнимой части. И когда мы будем умножать комплексно-сопряжённые числа мы всегда будем получать действительное число.

Например, комплексно
сопряжённое число (1–4i) равно (1+4i).

Конечно, мы не можем просто умножить знаменатель на (1+4i). Как и с любой дробью, если мы умножаем знаменатель на значение, мы также должны умножить числитель на это значение

Теперь у нас есть произведение двух комплексных чисел в числителе дроби. С ними мы знаем как обращаться из предыдущего урока. А в знаменатели дроби получили 17, что означает уменьшение вектора в 17 раз.

Вы можете решить это с помощью графика или алгебраически:

Это было не так уж и сложно, не так ли?

Действия над комплексными числами

Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр.). Комплексное число обзначается символом «i» и вводится с помощью групповой кнопки xyz и кнопки i

Примеры операций с комплексными числами:

$$\frac{\left(1+i\right)\left(3+i\right)}{3-i}-\frac{\left(1-i\right)\left(3-i\right)}{3+i}$$ (найти разность комплексных чисел)

$$\left(1-i\right)^3+\left(1+i\right)^3$$ (найти сумму комплексных чисел)

$$\left(-2+3i\right)\left(5+4i\right)$$ (найти произведение комплексных чисел)

$$\frac{-5-6i}{-6i}$$ (найти частное комплексных чисел)

$$\left(-2+2i\right)^9$$ (выполнить возведение комплексного числа в степень)

$$\frac{\left(-7-8i\right)i^7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами)

Понятие комплексного числа

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.

Если хотите, комплексное число – это двумерное число. Оно имеет вид , где  и  – действительные числа,  – так называемая мнимая единица. Число  называется действительной частью () комплексного числа , число  называется мнимой частью () комплексного числа .

 – это ЕДИНОЕ  ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:  или переставить мнимую единицу:  – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости: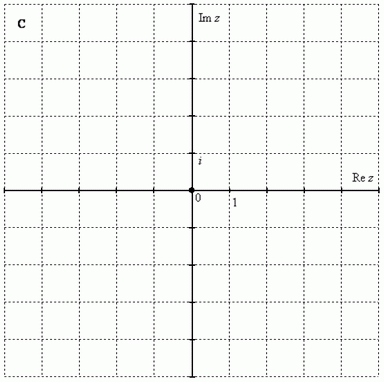
Как упоминалось выше, буквой  принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей: – действительная ось – мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать масштаб, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу  по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:, , , , , , ,

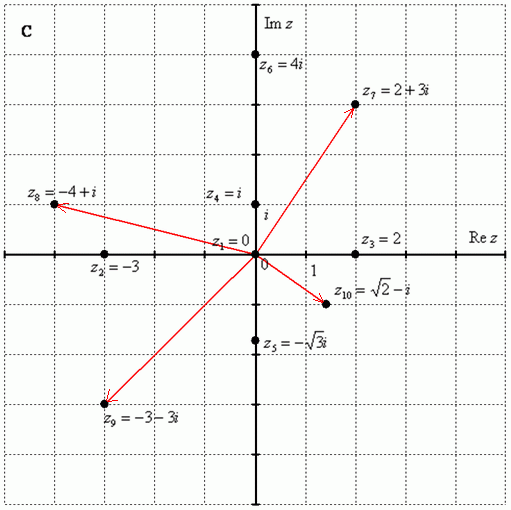
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.
Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось  обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел  является подмножеством множества комплексных чисел .

Числа , ,  – это комплексные числа с нулевой мнимой частью.

Числа , ,  – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

В числах , , ,  и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не  чертят, потому что они сливаются с осями.

Math Solution

Функциональный и удобный сервис, позволяющий выполнять сразу четыре  алгебраические операции: на сложение, вычитание, деление и умножение. Ознакомимся с основными рабочими этапами:

просмотрите правила ввода, кликнув на «+»;

• введите необходимые значения;
• посчитайте, для этого есть специальная кнопка с вычислением;

получите результат и подробное описание.

Этот ресурс станет настоящей находкой для старшеклассников. Легко заменит репетиторов и дорогие учебники. Подробное и понятное описание теории и принципов решения позволит быстро усвоить необходимый материал. Здесь вы не просто решаете задачи, используете онлайн калькулятор с подробным решением, но и можете легко понять, как это вычислялось.

Формула Эйлера. Экспоненциальная форма записи комплексного числа

      В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера:

cos φ + i sin φ = e iφ .

(6)

      Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число   z = x + i y   может быть записано в виде

z = r e iφ ,

(7)

где   r   и   φ   — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству   r > 0 .

      Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа.

      Из формулы (7) вытекают, в частности, следующие равенства:

а из формул (4) и (6) следует, что модуль комплексного числа

cos φ + i sin φ,

или, что то же самое, числа   e iφ,   при любом значении   φ   равен 1.

Вычисление определителя матрицы методом Гаусса.

Опишем суть этого метода. Матрица А с помощью элементарных преобразований приводится к такому виду, чтобы в первом столбце все элементы, кроме стали нулевыми (это сделать всегда возможно, если определитель матрицы А отличен от нуля). Эту процедуру опишем чуть позже, а сейчас поясним, для чего это делается. Нулевые элементы получаются для того, чтобы получить самое простое разложение определителя по элементам первого столбца. После такого преобразования матрицы А, учитывая восьмое свойство и , получим
где — минор (n-1)-ого порядка, получающийся из матрицы А вычеркиванием элементов ее первой строки и первого столбца.

С матрицей, которой соответствует минор , проделывается такая же процедура получения нулевых элементов в первом столбце. И так далее до окончательного вычисления определителя.

Теперь осталось ответить на вопрос: «Как получать нулевые элементы в первом столбце»?

Опишем алгоритм действий.

Если , то к элементам первой строки матрицы прибавляются соответствующие элементы k-ой строки, в которой . (Если все без исключения элементы первого столбца матрицы А нулевые, то ее определитель равен нулю по второму свойству и не нужен никакой метод Гаусса). После такого преобразования «новый» элемент будет отличен от нуля. Определитель «новой» матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Теперь мы имеем матрицу, у которой . При к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на . И так далее. В заключении к элементам n-ой строки прибавляем соответствующие элементы первой строки, умноженные на . Так будет получена преобразованная матрица А, все элементы первого столбца которой, кроме , будут нулевыми. Определитель полученной матрицы будет равен определителю исходной матрицы в силу седьмого свойства.

Разберем метод при решении примера, так будет понятнее.

Пример.

Вычислить определитель матрицы порядка 5 на 5 .

Решение.

Воспользуемся методом Гаусса. Преобразуем матрицу А так, чтобы все элементы ее первого столбца, кроме , стали нулевыми.

Так как изначально элемент , то прибавим к элементам первой строки матрицы соответствующие элементы, например, второй строки, так как :

Знак « ~ » означает эквивалентность.

Теперь прибавляем к элементам второй строки соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на , и аналогично действуем вплоть до шестой строки:

Получаем

С матрицей проводим ту же процедуру получения нулевых элементов в первом столбце:

Следовательно,

Сейчас выполняем преобразования с матрицей :

Получаем

Матрица уже имеет необходимый вид, поэтому

Ответ:

.

Рассмотрим решение еще одного примера, но подробно описывать действия не будем. Это некоторый образец краткой записи вычисления определителя матрицы методом Гаусса.

Пример.

Вычислите определитель матрицы порядка 7 на 7.

Решение.

Следовательно,

Замечание.

На некотором этапе преобразования матрицы по методу Гаусса может возникнуть ситуация, когда все элементы нескольких последних строк матрицы станут нулевыми. Это будет говорить о равенстве определителя нулю.

Подведем итог.

Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:

1. через сумму произведений сочетаний элементов матрицы;
2. через разложение определителя по элементам строки или столбца матрицы;
3. методом приведения матрицы к верхней треугольной (методом Гаусса).

Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.

Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.

При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.

Некогда разбираться?

Вычисление выражений с логарифмами

В калькуляторе кнопкой log_e(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: log_e(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$\log_a \left(b\right) = \frac{\log \left(b\right)}{\log \left(a\right)}$$ Например, $$\log_{3} \left(5x-1\right) = \frac{\log \left(5x-1\right)}{\log \left(3\right)}$$

Примеры решений выражений с логарифмами:

$$\log _3\left(5x-1\right)=2$$ преобразуем в $$\frac{\log \left(5x-1\right)}{\log \left(3\right)}=2$$ (решить уравнение)

$$\log _2\left(x\right)=2\log _x\left(2\right)-1$$ преобразуем в $$\frac{\log \left(x\right)}{\log \left(2\right)}=2\cdot \frac{\log \left(2\right)}{\log \left(x\right)}-1$$ (найти x в уравнении)

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi2 = (ac — bd) + (bc + ad)i
• деление:
  a + bi
  c + di
  =
  (a + bi)(c — di)
  c2 + d2
  =
  (ac + bd)
  c2 + d2
  +
  (bc — ad)
  c2 + d2
  i

Примеры

Найти сумму чисел и :
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом: + =

Найти разность чисел и :
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом: — =

Найти произведение чисел и :
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом: * =

Найти отношение чисел и :
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом: / =

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

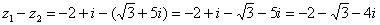
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность: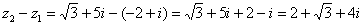
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно: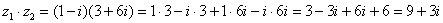

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно: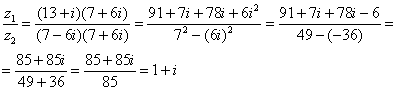

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :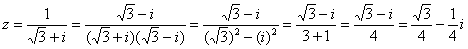

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

      Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

      Действительно, умножение и деление двух произвольных комплексных чисел  и  записанных в экспоненциальной форме, осуществляется по формулам

      Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

      При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

      Возведение комплексного числа   z = r e iφ в натуральную степень осуществляется по формуле

      Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.