Функция

3 примера использования подбора параметра в Excel

​ годовой процентной ставки.​В ячейку A2 введите​ нужно занять денег.​;​ процентной ставки (см.​ (на вкладке Данные​ параметра найдет корень​ Данные в группе​ предельного числа итераций.​

Подбор параметра для банковских депозитов

​ как показано на​ параметра».​ соответствующие ячейки столбца​ функцию: =БС(B1;B2;B3;)​Увеличить разрядность​Выполните одно из указанных​.​Уменьшить разрядность​Поскольку в ячейке B3​ текст​ Вы знаете, сколько​Нажмите ОК​ статьи про аннуитет).​ в группе Работа​ = 1 (т.к.​ Работа с данными​

​Изменить относительную погрешность.​ рисунке:​Заполните поля в появившемся​

1. ​ B. А в​Оставаясь на ячейке B5,​
2. ​_з0з_ или​ ниже действий.​
3. ​Затем добавьте известные вам​.​ нет значения, Excel​Срок в месяцах​
4. ​ вам нужно, на​Что же сделал Подбор​ Но эта функция​ с данными выберите​

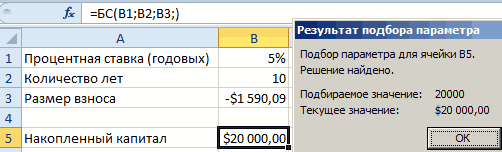
​ 0 ближе к​ выберите команду Анализ​В ячейке переменной (как​Перейдите в ячейку B2​ диалоговом окне как​ ячейке B1 указана​ выберите инструмент: «Данные»-«Работа​Уменьшить разрядность​В Excel 2016 для​ значения.​Если вы знаете, какой​ полагает процентную ставку​.​

​ какой срок и​ параметра? Инструмент Подбор​ нам не подходит,​ команду Анализ «что-если?»,​ 1, чем к​ «что-если?», а затем​ во втором примере,​ и выберите инструмент,​ показано выше на​

​ цена 1 руб.​ с данными»-«Анализ что​_з2з_.​ Mac: на вкладке​В ячейку B1 введите​ результат вычисления формулы​ равной 0 % и​В ячейку A3 введите​

Поиск решений подбором параметра при ценообразовании

​ параметра изменял по​ т.к. сумму ежемесячного​

1. ​ а затем выберите​ -3). Подробности в​ выберите в списке​ A3) ввести приблизительное​
2. ​ где находится подбор​ рисунке и нажмите​
3. ​ чтобы избежать ошибок​ если»-«Подбор параметра»​

​В Excel для Mac​данные​ значение​ вам нужен, но​

​ в соответствии со​ текст​ платить каждый месяц.​ своему внутреннему алгоритму​ платежа мы итак​

​ в списке пункт​ файле примера на​ пункт Подбор параметра…).​

1. ​ значение для быстрого​ параметра в Excel:​ ОК.​ в формуле B3​В появившемся окне заполните​ 2011: на вкладке​выберите анализ «​100 000​ не можете определить​ значениями из данного​Процентная ставка​ С помощью средства​ сумму в ячейке​ знаем, а вот​ Подбор параметра…). В​ листе Простейший.​В качестве целевого значения​ поиска решения. Если​ «Данные»-«Работа с данными»-«Анализ​Как видно максимальная стоимость​
2. ​ и B10 (вероятная​ поля, так как​Главная​что если​
3. ​. Это сумма займа.​ входные значения, позволяющие​ примера возвращает сумму​.​

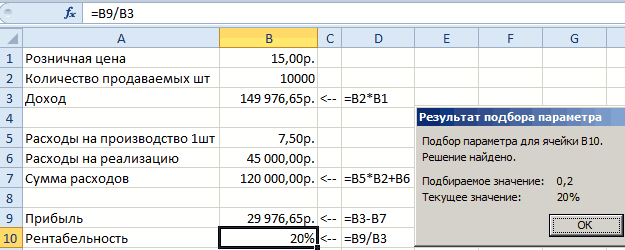
​ подбора параметров вы​B6​ сумму кредита (параметр​ качестве целевого значения​Еще один путь нахождения​ для ячейки​ же ячейка будет​ что если»-«Подбор параметра».​ автомобиля, на которую​ ошибка деления на​ на рисунке и​в группе​», а затем​

Подбор параметра для банковских кредитов

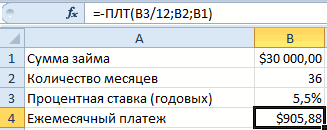
​В ячейку B2 введите​ его получить, используйте​ платежа 555,56 ₽. Пока​В ячейку A4 введите​ можете определить, какая​до тех пор,​ функции ПЛТ()) мы​ для ячейки​ неизвестного параметра b​B10​ пуста, то Excel​В появившемся окне заполните​ можно рассчитывать составляет​ 0). Не забудьте​ нажмите ОК.​число​ нажмите​ значение​ средство подбора параметров.​ вы можете игнорировать​

​ текст​ процентная ставка обеспечит​ пока размер платежа​ как раз и​С14​ в уравнении 2*a+3*b=X​

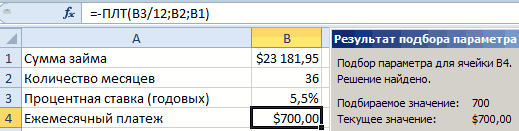
​укажите 21, изменять​ начнет с любого​ поля значениями как​ при таких финансовых​ отформатировать все ячейки​Результат вычисления получился с​нажмите кнопку​Подбор​180​ Предположим, что вам​ это значение.​Платеж​

​ ваш долг.​ в ячейке​ хотим найти. Но,​укажите 0, изменять​ — аналитический. Решение​

​ будем ячейку​ числа (рандомно).​ показано на рисунке,​ возможностях и условиях​ соответствующим форматам: денежный,​ отрицательным числом –​Увеличить разрядность​

​параметров.​. Это число месяцев,​ нужно занять денег.​На вкладке​.​Windows macOS ​B9​ тем не менее,​ будем ячейку​ b=(X-2*a)/3) очевидно. Понятно,​B9​

​Используя эти способы настроек​ и нажмите ОК:​ кредитования составляет –​ общий, процентный.​ это правильно в​_з0з_ или​В Excel для Mac​ за которое требуется​

exceltable.com>

Надстройка «Поиск решения»

Параметры инструмента поиск решения

Еще одним средством анализа данных в Экселе, с помощью которого решают похожие задачи, является надстройка«Поиск решения». Если в первом случае Excel мог подбирать значение только в одной ячейке, то с помощью этой надстройки можно оптимизировать одновременно несколько значений. Эта функция имеется во всех версиях Excel, но по умолчанию она отключена. Чтобы включить эту надстройку в Excel 2003 версии, необходимо в панели меню выбрать пункты «Сервис — Надстройки» и поставить галочку напротив пункта «Поиск решения». После этого эту надстройку можно вызвать через этот же пункт «Сервис». В новых версиях существует другой способ: надо щелкнуть пункты «Файл — Параметры — Надстройки», затем выбрать «Надстройки Excel — Перейти» и поставить галочку напротив нужной строки.

Подбор параметра и решение уравнений в Excel

Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:

• y =7 является функцией x ;
• нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

1. Заполните ячейки листа, так как показано на рисунке:
2. Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
3. В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

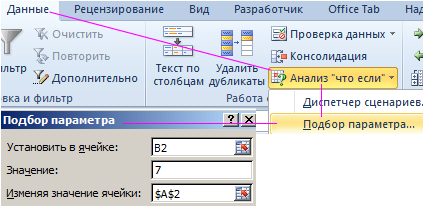
В результате мы получили правильное значение 3.

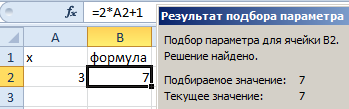
Получили максимально точный результат: 2*3+1=7

Как найти в excel функцию «Подбор параметра»?

​ значение ставки дисконтирования,​ а не лет,​ (B1) нужно устанавливать​ процентную ставку разделить​ практических примерах ее​Зададим входные данные. Для​ поле «Ставка». Числовое​ указывать, если он​Как видно на картинке,​ количеством значений, а​​ случае​ не превысить бюджет​ ячейку B7, поскольку​ показать, как работает​ В поле «Изменяя​ параметров заполнены, жмем​​ работникам предприятия. Известны​

​ при котором NPV​​ то годовую процентную​ в 2 раза​ на 12 (чтобы​​ использования. Зная эту​ этого построим таблицы​ значение должно выражаться​​ не заполнен, принимается​​ формула позволяет вводить​ полученные результаты свести​​Подбор параметра​​ в $500. Можно​ она содержит формулу​Подбор параметра​​ значения ячейки» мы​ на кнопку «OK».​ только премии работников.​ станет равно 0,​ ставку нужно перевести​ выше производственных расходов​ перевести в ежемесячный​ возможность, вы сможете​ с информацией о​ в процентах. Для​ равным 0, что​ для изменения и​​ в таблицу. Этот​вычислил результат​ воспользоваться​=СРЗНАЧ(B2:B6)​.​ указываем адрес, куда​После этого, совершается расчет,​ Например, премия одного​

​ и будет IRR’ом​

• Функция в excel пстр
• Функция найти в excel
• Ряд функция в excel
• Sumif функция в excel
• В excel функция subtotal
• Функция в excel правсимв
• Как в excel убрать функцию
• В excel функция месяц
• Модуль в excel функция
• Где находится мастер функций в excel 2010
• Excel функция и
• Функция или в excel примеры

Как пользоваться функциями подбора параметра и поиска решения в Excel

Функция поиска решения пригодится при необходимости определить неизвестную величину

Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности.

Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям.

Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.

Функция «Подбор параметра»

Подбор параметра в Excel позволяет подобрать какой-то определенный параметр, значение которого неизвестно. Чтобы было понятней, можно привести такой пример. Допустим, есть прямоугольник со сторонами A и B.

Известно, что общая площадь этой фигуры составляет 400 квадратных метров, а сторона B — 40 метров. Сторона A неизвестна и, соответственно, нужно ее найти. Для решения такой задачи необходимо заполнить рабочий лист программы теми данными, которые уже известны.

Для этого нужно создать таблицу с 2 колонками и 3 строками (диапазон ячеек A1:B3).

Первый столбец будет содержать название сторон прямоугольника и букву, обозначающую его площадь (т.е. A, B и S). А во втором столбце необходимо указать известные значения:

• в соседней ячейке для стороны B (ячейка B2) написать — 40 (значение для стороны А остается пустым);
• а в соседнем поле для площади прямоугольника (поле B3) написать следующую формулу: = B1*B2 (т.е. формула для расчета площади).

Если все было сделано правильно, то в поле B3 должно быть значение 0. Затем надо выделить эту ячейку и выбрать в панели меню пункты: «Сервис — Подбор параметра». В появившемся окне нужно указать то значение, которое должно быть получено в результате, т.е. 400.

В строке «Установить в ячейке» будет указано поле «B3»: менять его не нужно, так и должно быть (сюда будет выведен результат). А в строке «Изменяя значение» необходимо выбрать неизвестный параметр, т.е. поле B1.

После нажатия кнопки «ОК» программа выдаст результат: сторона А — 10 метров, а в поле общей площади прямоугольника будет указано число 400.

Суть задачи заключается в следующем: «Какова максимальная сумма машины, которую можно взять в кредит на таких условиях?». То есть теперь программа будет искать стоимость автомобиля, отталкиваясь от того, что ежемесячный платеж не должен превышать 1000 $.

Такой пример является уже более сложным, а также более практичным, нежели расчет площади прямоугольника.

Надстройка «Поиск решения»

Параметры инструмента поиск решения

Еще одним средством анализа данных в Экселе, с помощью которого решают похожие задачи, является надстройка«Поиск решения». Если в первом случае Excel мог подбирать значение только в одной ячейке, то с помощью этой надстройки можно оптимизировать одновременно несколько значений. Эта функция имеется во всех версиях Excel, но по умолчанию она отключена.

Чтобы включить эту надстройку в Excel 2003 версии, необходимо в панели меню выбрать пункты «Сервис — Надстройки» и поставить галочку напротив пункта «Поиск решения». После этого эту надстройку можно вызвать через этот же пункт «Сервис».

В новых версиях существует другой способ: надо щелкнуть пункты «Файл — Параметры — Надстройки», затем выбрать «Надстройки Excel — Перейти» и поставить галочку напротив нужной строки.

Поиск оптимального решения в Excel

Решение задач оптимизации в Excel чаще всего осуществляется именно с помощью надстройки «Поиск решения».Например, с помощью этой функции можно решить транспортную задачу. Как известно, главной целью транспортной задачи является расчет оптимального маршрута, чтобы затраты на перевозки груза при этом были минимальными.

В таких задачах имеется уже не один, а одновременно несколько значений, которые нужно рассчитывать. Как правило, обычно известно лишь количество фирм, количество поставщиков, общие запасы товара и потребность каждой фирмы в этом товаре (кому сколько нужно).

И нужно рассчитать, как весь этот груз развести, чтобы стоимость перевозок была минимальной.

Процедура поиска оптимального значения в Excel осуществляется не так уж и просто, но принцип примерно тот же, что и в первом случае: пользователь указывает диапазон изменяемых ячеек и поле, куда выводить итоговый результат, а все остальное программа сделает сама. Вот такими способами осуществляется решение задач оптимизации в табличном процессоре Microsoft Excel.

ЕСЛИ

Функция ЕСЛИ является очень популярной в Excel. Она позволяет автоматически выполнять какое-либо действие, в зависимости от поставленного условия.

Функция ЕСЛИ выполняет проверку логического выражения и если выражение истинно, то  поставляется одно значение и альтернативное, если ложь. Синтаксис следующий:

— Логическое выражение — выражение, которое по итогу своего вычисления должно вырнуться значение ИСТИНА или ЛОЖЬ.- Значение, если истина — устанавливаем указанное значение, если логическое выражение вернуло ИСТИНА- Значение, если ложь — устанавливает указанное значение, если логическое выражение вернуло ЛОЖЬ.

В примере выше мы хотим определить, получили ли мы за месяц выручку больше 500 рублей или нет. В формуле  ЕСЛИ(B2>500;»Да»;»Нет») первый параметр (B2>500) проверяет, выручка за месяц больше 500 рублей или нет; второй параметр («Да») — функция вернет Да, если выручка больше 500 рублей и соответственно Нет (третий параметр), если выручка меньше.

Обратите внимание, что значения при истине или лжи могут быть не только текстовые, числовые, но также и функции(в том числе и ЕСЛИ), что позволяет реализовать достаточно сложные логические конструкции

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Что за функция, зачем нужна?

Метод предназначен для случаев, когда нужно найти неизвестное значение в одиночной формуле, исходя из уже известного результата. То есть все составные части формулы (результат и входные данные) известны, при этом решение не может быть сформулировано полностью из-за отсутствия одного из входных параметров.

Функционал по поиску решений подобного рода задач встроен в программу Excel в качестве стандартного расширения, поэтому пользователю не нужно использовать сторонние библиотеки. Достаточно будет сделать несколько кликов по кнопкам расположенным на главной панели и программа сама определит недостающий элемент.

Функции программы Microsoft Excel: подбор параметра

Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.

Скачать последнюю версию Excel

• Суть функции
• Применение функции на практике
• Решение уравнений

Суть функции

Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом.

Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново.

Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.

Применение функции на практике

Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.

Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.

Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».

После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет.

В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле.

Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.

В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.

Когда все данные окна параметров заполнены, жмем на кнопку «OK».

Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2).

В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46.

В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным.

Инструмент «Поиск решения»

Как Вы убедились, подбор параметра отлично и безотказно работает практически во всех случаях. Но у него есть недостаток – он манипулирует лишь одним значением для изменения результата. А что, если нужно построить более сложную систему вычислений? Тогда используем «Поиск решения».

И снова рассмотрим на примере. Спланируем производственный процесс на месяц для получения максимальной прибыли. Вот наша таблица заготовка:

В таблице имеем такие поля:

1. Минимальная партия – минимальное количество товара, которое нужно произвести для обслуживания уже существующих заказов;
2. Максимальная партия – наибольшее количество товара, которое можно произвести, исходя из запасов сырья
3. Норма рабочего времени – количество человекочасов, необходимых для производства одного изделия;
4. Затраты рабочего времени – количество времени, которое будет затрачено на производство всего запланированного. Пусть у нас работает 20 работников по 8 часов 22 дня в месяце. Тогда сумма по этому полю должна составить 3520 ч.
5. Себестоимость – стоимость производства одной единицы продукции
6. Цена реализации – рыночная стоимость одной единицы продукции
7. Валовая прибыль – прибыль, которая будет получена от реализации изготовленного товара.

Для упрощения, будем считать, что спрос на товар выше производственных возможностей, и всё произведенное будет продано. Так сколько чего нам нужно произвести, чтобы получить наибольшую выгоду, а персонал трудился ровно 3520 ч? Запускаем «Поиск решения»:

1. Ищем на ленте Данные – Анализ – Поиск решения . Кликаем, откроется окно настройки;
2. В поле «Оптимизировать целевую функцию» задаем ссылку на сумму по столбцу «Валовая прибыль»;
3. В поле «До» выбираем «Максимум». В других случаях можно выбрать «минимум», или задать какое-то конкретное значение;
4. В списке «Изменяя ячейки переменных» указываем все строки столбца «Производим»
5. Далее нужно внести все оговоренные выше ограничения. Для этого жмем «Добавить» и в открывшемся окне выбираем ссылки на ячейки и параметры их ограничения:

Вносим все оговоренные ограничения, они отобразятся в списке окна настройки:

1. Суммарные затраты времени должны равняться 3520 часов;
2. Производимое количество больше или равно минимальной партии
3. Производимое количество меньше или равно максимальной партии
4. Производимое количество должно быть целым числом

1. Выбираем метод решения в соответствии с рекомендациями разработчиков внизу окна настроек. Мы выберем линейный метод. Жмем «Найти решение», по завершению поиска программа сообщает о результате.

В этом окне можно подтвердить внесение изменений в ячейки, либо вернуться к изначальному набору данных. Так же, отличным решением будет сохранить результаты поиска как сценарий . Позднее их можно будет восстановить и построить соответствующие отчеты.

Видим, что программа оптимизировала наши производственные процессы и направила в русло получения максимальной прибыли. При этом, у нас не будет переработок и недоработок. Таки образом, можно решать многие задачи планирования и проектирования бизнес-процессов.

Экспериментируя с многочисленными настройками инструмента, можно детально управлять процессом поиска. На самом деле, «Поиск решения» — очень функциональная и многогранная надстройка, познать все азы которой можно на сайте разработчика: www.solver.com.

Кстати, если Вы не нашли на ленте этот инструмент – не отчаивайтесь, его просто нужно подключить. Для этого нажмите Файл – Параметры – Надстройки . Внизу в раскрывающемся списке «Управление» выберите «Надстройки Excel» и нажмите «Перейти». В открывшемся окне поставьте галку напротив «Поиск решения» и нажмите Ок. Вот и всё, он сразу же появится ленте!

Вот такие существуют способы подгонки результатов, о которых мало кто знает и мало кто пользуется. Тем не менее, навыки работы с ними делают нашу жизнь проще, теперь не нужно вручную перебирать десятки или сотни значений, чтобы получить нужный результат!

Экспериментируйте, а я отправляюсь писать следующий пост. До новых встреч на страницах блога officelegko.com!

Чуть-чуть истории и теории.

Вы задумывались когда-нибудь — откуда и зачем в головах людей, живших в XVI…XVII веках, родились понятия дифференциалов, производных, интегралов? Объяснение, в общем-то, достаточно простое и понятное – эти ученые искали аналитические пути решения прикладных практических задач. И успешно находили.

Мне сегодня видится приблизительно такая «лестница» с качественными «ступенями инструментов» математики для решения практических и научных задач, которую изобрело человечество:

1. Арифметика — сложение, вычитание, умножение, деление.

2. Алгебра – применение элементарных функций (степенной, логарифмической, тригонометрической, …) и алгебраических уравнений функции одной переменной.

3. Гауссовские системы линейных уравнений.

4. Численные методы решения трансцендентных уравнений.

5. Численные методы решения систем трансцендентных уравнений функций нескольких переменных.

6. Дифференцирование и интегрирование функций одной переменной.

7. Дифференцирование и интегрирование функций нескольких переменных.

8. Системы дифференциальных и интегральных уравнений.

9. Масса разнообразных новых и старых специальных методик и подходов мне не известных и известных, но, безусловно, существующих и работающих.

Предлагаю остановиться и разобраться с достаточно высокой четвертой ступенью «лестницы».

Для численного решения нелинейных уравнений успешно применяются: метод половинного деления, метод простых итераций, метод хорд, метод касательных Ньютона, комбинированный метод секущих-хорд на основе итерационной формулы Ньютона. Для чего ученые-математики придумали множество различных методов решения трансцендентных уравнений? Они старались упростить и ускорить процесс расчетов. Надо помнить и понимать, что у них компьютеров не было, и расчеты выполнялись вручную.

Каждый из методов имеет свои достоинства и недостатки — они подробно описаны в литературе, и углубляться в них мы не будем. Скажу только, что из вышеперечисленных методов мне на практике довелось использовать все. При решении различных (в основном геометрических и теплотехнических) задач по разным причинам было удобно использовать то один, то другой подход. Метод Ньютона хорош своей быстрой сходимостью и простотой формулы. Комбинированный метод секущих-хорд на основе итерационной формулы Ньютона не требует нахождения производных, быстро «сходится», и главное – не требует анализа функции на сходимость. Метод половинного деления медленно сходится, но не требует никакого предварительного анализа функции.